Question

Дифференциальное уравнение 1-го порядка решить,очень нужно!(

Answer 1

$y=arctgx +Ce^{-arctgx}-1$

Пошаговое объяснение:

$(1+x^2)y'+y=arctgx$

Разделим всё уравнение на 1+х², (1+x²>0)

$y'+\frac{y}{1+x^2} =\frac{arctgx}{1+x^2}$

Это уравнение первого порядка называется линейным, так как оно имеет вид: y'+P(x)y=Q(x), где P(x)=1/(1+x²); Q(x)=arctgx/(1+x²)

Его можно решать, например, методом Бернулли:

Сделаем подстановку: y=uv; y'=u'v+uv'

подставим в уравнение:

$u'v+uv'+\frac{uv}{1+x^2}=\frac{arctgx}{1+x^2}$

Далее выносим из 2-го и 3-го слагаемых общий множитель u за скобки (так делается всегда)

$u'v+u\left(v'+\frac{v}{1+x^2}\right)=\frac{arctgx}{1+x^2} \ \ (*)$

то что получилось в скобках приравниваем к нулю:

$v'+\frac{v}{1+x^2}=0$

Полученное уравнение является ДУ с разделяющимися переменными. Нам нужно найти его какое нибудь одно частное решение. Самое простое - это при решении опустить константу С (то есть принять С=0)

$v'+\frac{v}{1+x^2}=0 \ \Rightarrow \ \frac{dv}{dx}=-\frac{v}{1+x^2} \ \ |\cdot \frac{dx}{v} , \ v \neq 0 \ \Rightarrow \ \frac{dv}{v}=-\frac{dx}{1+x^2} \ \Rightarrow \\ \\ \Rightarrow \ \int\frac{dv}{v}=-\int\frac{dx}{1+x^2} \ \Rightarrow \ \ln|v|=-arctgx \ \Rightarrow \ v=e^{-arctgx}$

Подставляем найденное v в уравнение (*) и так же не забываем, что результат в скобках равен нулю:

$u'e^{-arctgx}+u \cdot 0=\frac{arctgx}{1+x^2} \ \Rightarrow \ \frac{du}{dx} e^{-arctgx}=\frac{arctgx}{1+x^2} \ \ |\cdot e^{arctgx}dx \ \Rightarrow \\ \\ \Rightarrow \ du=e^{arctgx} \cdot \frac{arctgx}{1+x^2} dx \ \Rightarrow \ \int du=\int arctgx\cdot \frac{e^{arctgx}}{1+x^2} dx \ \Rightarrow \ \\ \\\Rightarrow \ u=\int arctgx\cdot \frac{e^{arctgx}}{1+x^2} dx \ \Rightarrow \ (**)$

полученный интеграл берем по частям: где U=arctgx и dV=e^(arctgx)/(1+x^2)dx

Поэтому прежде стоит найти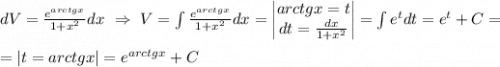$dV=\frac{e^{arctgx}}{1+x^2}dx \ \Rightarrow \ V=\int\frac{e^{arctgx}}{1+x^2}dx=\begin{vmatrix} arctgx=t \\ dt=\frac{dx}{1+x^2} \end{vmatrix} =\int e^t dt=e^t+C =\\ \\ = |t=arctgx|=e^{arctgx}+C$ V

Теперь возвращаемся к решению (**)

$u=\int arctgx\cdot \frac{e^{arctgx}}{1+x^2} =\begin{vmatrix}U=arctgx; \ dV=\frac{e^{arctgx}}{1+x^2}dx \\dU=\frac{dx}{1+x^2}; \ V=e^{arctgx} \end{vmatrix}=arctgx \cdot e^{arctgx}- \\ \\ -\int \frac{e^{arctgx}}{1+x^2}dx=arctgx \cdot e^{arctgx}- e^{arctgx}+C$

Осталось сделать обратную замену:

$y=uv=(arctgx \cdot e^{arctgx}-e^{arctgx}+C)\cdot e^{-arctgx}=\\ \\ =arctgx -1+Ce^{-arctgx}$

И на последнем шаге нужно выяснить, есть ли у данного ДУ особые решения.

Если внимательно посмотреть на ход решения, то можно заметить следующее:

когда мы решали уравнение

$\frac{dv}{dx}=-\frac{v}{1+x^2} \ \ |\cdot \frac{dx}{v} , \ v \neq 0$

все последующие действия были с учетом того, что v≠0.

Осталось проверить, будет ли начальное ДУ иметь решение, если v=0?

$y=uv=u\cdot 0=0 \\ \\ y=0 \ \Rightarrow \ y'=0 \\ \\ (1+x^2)y'+y=arctgx \\ \\ (1+x^2)\cdot 0+0=arctgx \\ \\ 0=arctgx$

Последнее равенство не является тождеством! (то есть равенство не выполняется для любых иксов, а только для конкретных). Значит особых решений нет.