
20
Пошаговое объяснение:
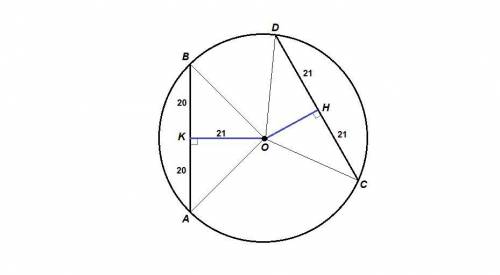
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и и OH⊥CD,
ОК = 21 - расстояние от центра до АВ,
ОН - искомое расстояние от центра до CD.
ΔОАВ равнобедренный, значит ОК - высота и медиана. ⇒
АК = КВ = 1/2АВ = 1/2 · 40 = 20
Из прямоугольного треугольника АКО по теореме Пифагора:
АО = √(АК² + КО²) = √(20² + 21²) = √(400 + 441) = √841 = 29
СО = АО = 29
ΔCOD равнобедренный, значит OН - высота и медиана, ⇒
СН = HD = 1/2CD = 1/2 · 42 = 21
Из прямоугольного треугольника СОН по теореме Пифагора:
OH = √(CO² - CH²) = √(29² - 21²) = √(841 - 441) = √400 = 20
Можна.
Позначимо:
ВС - ціна великого рака сьогодні
МС - ціна маленького рака сьогодні
ВУ - ціна великого рака учора
МУ - ціна маленького рака учора
Запишемо умову задачі:
3ВС + 1МС = 5ВУ (1)
2ВС + 1МС = 3ВУ + 1МУ (2)
Виразимо ВС через ВУ і МУ. Для цього віднімемо рівняння (2) від (1):
1ВС = 2ВУ - 1МУ (3)
Тепер виразимо МС через ВУ і МУ. Для цього помножимо рівняння (1) на 2, а рівняння (2) на 3:
6ВС + 2МС = 10ВУ (4)
6ВС + 3МС = 9ВУ + 3МУ (5)
і віднімемо (5) - (4):
1МС = - 1ВУ + 3МУ (6)
В задачі питається, що більше: 1ВС + 2МС чи 5ВУ?
Підставимо в 1ВС + 2МС отримані вирази (3) і (6):
1ВС + 2МС = (2ВУ - 1МУ) + 2(-1ВУ + 3МУ) = 2ВУ - 1МУ - 2ВУ + 6МУ = 5МУ
Отже 1ВС + 2МС = 5МУ
Відповідь: один великий та два маленькі сьогодні коштують стільки ж, як п'ять маленьких учора.