Пусть где-то стоит единица. Рядом с ней может стоять только 2 (пусть она стоит справа) и 3 (слева). Среди чисел от 1 до 100 встречаются чётные и нечётные числа. Очевидно, правее двойки могут стоять только чётные числа (Ч + 2 = Ч, Ч*2 = Ч), значит, слева от 3 должны быть все нечётные числа: 5, 7, 9, ..., 99. Получается, 99 встретится с каким-то чётным числом. Натуральным числом, отличающимся от 99 в два раза может быть только 198, что больше 100 (если число отличается на 2, то оно нечётное, поэтому этот случай не рассматриваем). Значит, такого быть не может.
ответ: нет
sqrt(2)
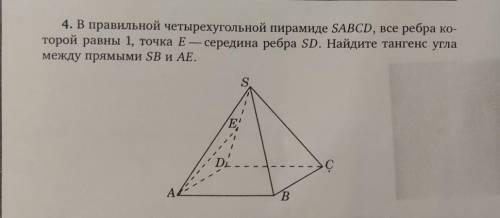
Пошаговое объяснение: Пусть М -середина DB.
MЕ||SB и MЕ=0,5 (средняя линия в треугольнике DBS). MЕ=0,5 AЕ=sqrt(3)/2 (высота в равностороннем треугольнике) AM=sqrt(2)/2 (половина диагонали квадрата)
AЕ^2=MЕ^2+AЕ^2. Значит треугольник МАЕ - прямоугольный. Угол ЕМА - прямой. Тангенс угла АЕМ равен АМ/ЕМ=sqrt(2). Так как MЕ||SB, тангенс равен искомому.
sqrt - корень квадратный