Відповідь:
414 обертів
Покрокове пояснення:
1 хвилина = 60 секунд
За 60 секунд швейна машина робить 1080 обертів. Щоб дізнатися скільки обертів робить машина за 23 секунди потрібно дізнатися скільки обертів швейна машина робить за 1 секунду. Тому потрібно кількість обертів (1080) поділити на час (60 секунд).
1080 : 60 = 18
Тобто за 1 секунду швейна машина робить 18 обертів. Тоді щоб знайти скільки обертів машина зробить за 23 секунди, потрібно 23 помножити на 18.
23 * 18 = 414 обертів
Даны координаты вершин пирамиды A1А2А3А4:
A1 (0, –1, 1), A2 (1, –6, 3), A3 (1, –5, 0), A4 (–2, 0, –2).
Найти: а) угол между ребрами A1А2 и A1А3;
x y z СумКвад. Длина ребра
Вектор А1А2={xА2-xA1, yА2-yA1, zА2-zA1} 1 -5 2 = √30 = 5,47723
Вектор А1А3={xА3-xA1, yА3-yA1, zА3-zA1} 1 -4 -1 = √18 = 4,24264.
cos A = (1*1 + (-5)*(-4) + 2*(-1)) / (6*√5) = 19/(√30*√18) = 19/√540 = 19/(6√15).
Угол А равен arc cos(19/(6√15) = 0,6135 радиан или 35,1518 градуса.
б) площадь грани A1 А2 А3;
Площадь грани A1 А2 А3 равна половине модуля векторного произведения:
S = (1/2)|A1А2*A1А3|.Координаты векторов найдены выше:
A1 A2: (1; -5; 2), A1 A3: (1; -4; -1).
i j k| i j
1 -5 2| 1 -5
1 -4 -1| 1 -4 = 5i + 2j - 4k + 1j + 8i + 5k =
= 13i + 3j + 1k.
Модуль равен √(13² + 3² +1²) = √179 ≈ 13,3791.
Площадь S = (1/2)* √179 ≈ 6,6895.
в) уравнение плоскости A1A2A3
Для составления уравнения плоскости используем формулу:
x – xA1 y – yA1 z – zA1
xА2 – xA1 yА2 – yA1 zА2 – zA1
xА3 – xA1 yА3 – yA1 zА3 – zA1 = 0
Подставим данные: A1 (0, –1, 1), A2 (1, –6, 3), A3 (1, –5, 0) и упростим выражение:
x - 0 y - (-1) z - 1
1 - 0 -6 - (-1) 3 - 1
1 - 0 -5 - (-1) 0 – 1 = 0
x y + 1 z - 1
1 -5 2
1 -4 -1 = 0
x * ((-5)·(-1)-2·(-4)) - (y + 1) * (1·(-1)-2·1) + (z - 1) * (1·(-4)-(-5)·1 = 0
13 x + 3 y + 3 + 1z - 1 = 0
13x + 3y + 1z + 2 = 0.
г) уравнение высоты, проходящей через A4;
Нормальный вектор плоскости А1А2А3 является направляющим вектором высоты из вершины А4 на грань A1А2А3.
Точка А4 (–2, 0, –2), вектор (13; 3; 1).
Уравнение высоты: (x + 2)/13 = y /3 = (z + 2)/1.
д) объём пирамиды.
Объём пирамиды V = (1/6)*|(A1А2xA1А3)*A1А4|.
A1А2xA1А3 = 13 3 1
А1А4 = -2 1 -3
A4 (–2, 0, –2) - A1 (0, –1, 1) = (-2; 1; -3).
(1/6)*|(A1А2xA1А3)*A1А4| = (1/6)*|(-26 + 3 - 3)| = 26/6 = 13/3 куб.ед.
Дано уравнение √(2x+4) = 1 - 2x.
ОДЗ: 2x + 4 ≥ 0, х ≥ -2,
1 - 2x ≥ 0, х ≤ 1/2.
Вывод: обе части его - положительны.
Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, в которой справедливо равенство (если оно существует).
Возведём его в квадрат: 2x + 4 = 1 - 4x + 4x².
4x² - 6x - 3 = 0. Д = 36 + 4*4*3 = 84. √84 = 2√21.
х1 = (6 + 2√21)/8 = (3 + √21)/4 ≈ 1,89564. По ОДЗ не принимаем.
х2 = (6 - 2√21)/8 = (3 - √21)/4 ≈ -0,39564.
ответ: корень один и равен х = (3 - √21)/4 ≈ -0,39564.
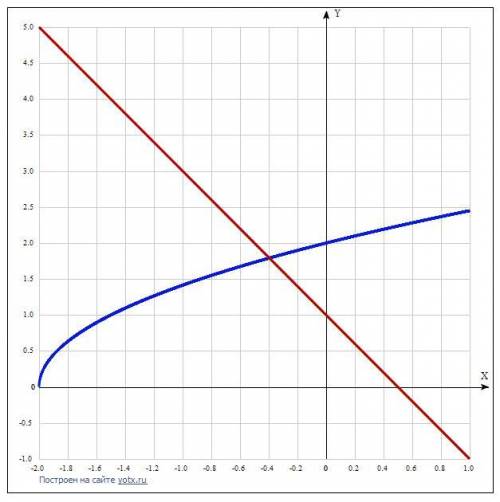
ответ можно подтвердить графически: ведь корень - это точка пересечения двух графиков у = √(2x+4) и у = 1 - 2x.
1080:60*23= 414
ответ: 414 оборотов сделал вал за 23 секунды