Пошаговое объяснение:
Трапеция АВСД
АВ=ВС=x – меньшие стороны образуют прямой угол.
Вторая сторона x+d
Третья x+d+d=x+2d
Наибольшая сторона – основание АД.
Почему?
Проводим высоту из точки С на сторону АД
Возможны два варианта
CД=x+d; АД=х+2d
ИЛИ
CД=x+2d; АД=х+d
В прямоугольном треугольнике СКД проверяем справедливость теоремы Пифагора.
В первом случае:
x2+(2d)2=(x+d)2 ⇒
x2+4d2=x2+2xd+d2 ⇒
3d2=2xd
3d=2x
Во втором случае:
x2+d2=(x+2d)2 ⇒
2xd+3d2=0
x>0; d>0 сумма двух положительных чисел равна 0, возможно когда каждое слагаемое равно 0
d=0 нет никакой прогрессии
Теперь используем условие про периметр:
x+x+(x+d)+(x+2d)=144
4x+3d=144
4x+2x=144
6x=144
x=24
d=2x/3=16
x+d=40
x+2d=56
24+24+40+56=144 – все верно
Наибольшая 56
Пошаговое объяснение:
1) определим тип кривой и приведем к каноническому виду.
y² - 2y + 3x - 3 = 0
Приводим квадратичную форму
B = y²
к главным осям, то есть к каноническому виду.
матрица этой квадратичной формы:
0 0
0 1
находим собственные числа и собственные векторы этой матрицы:
(0 - λ)x₁ + 0y₁ = 0
0x₁ + (1 - λ)y₁ = 0
характеристическое уравнение:
![\left[\begin{array}{ccc}1-\lambda&0\\0&1-\lambda\\\end{array}\right] =\lambda^2-\lambda=0](/tpl/images/1628/0993/2eba0.png)
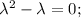 ⇒
⇒ 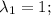
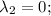
итак, мы имеем параболу 
обшее уравнение канонического вида
(y - y₀)² = 2p(x - x₀)
выделим в нашем уравнении полный квадрат для у
(y² -2y +1) +3x -3 -1 =0
(y-1)² = -3x -4
теперь нам надо справа выделить 2р и (х -х₀)
(y-1)² = 2*(-3/2)(x -4/3) - это и есть канонический вид заданного уравнения
теперь точки пересечения
мне удобнее решать систему
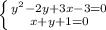
із второго выразим х и подставим в первое
x = -y -1
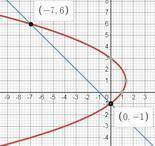
y²-2y+3(-y-1) -3=0; y² -5y -6 = 0; ⇒ y₁ = 6; y₂= -1 ⇒ х₁ = -6-1=-7; х₂ = -(-1)-1 =0
вот это получились наши точки пересечения
М₁(-7;6) М₂(0; -1)
1226=1200
1226=1000