1) -3
2) 0
3) ∞
Пошаговое объяснение:
Для вычисления предела на бесконечности частного двух многочленов можно сравнить степени многочленов - если степень числителя больше, то предел частного будет равен бесконечности. если степени одинаковые, то предел будет равен отношению коэффициентов при старших степенях. Если степень в значменателе больше, то предел будет равен нулю. Примеры на все три случая:
1) 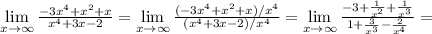
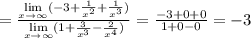
2) 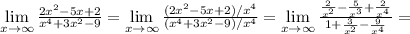
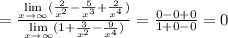
3)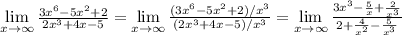
В числителе стоит бесконечно большая функция, знаменатель стремится к 2 (то есть имеет конечный предел), значит частное будет бесконечно большим.
Пошаговое объяснение:
80) -14+36=22
81) 15+(-8)=7
82) -1+12=11
83) -17+9=8
84) -5+(-10)=15
85) 40+(-30)=10
86) -81+(-19)=100
87) -34+10=24
88) -8+12=4
89) 19+(-3)=16
90) -6+11=5
91) -32+(-4)=36
92) 3,7-5,6=-1,9
93) -4,7+2,9=1,8
94) 5,2-3,7=1,5
95) -6,4-3,6=10
96) 9,7+(-9,8)=0,1
97) 8+(-25)=17
98) -6+(-11)=-17
99) 47+(-60)=-13
100) 26+(-37)=-11
101) -23+93=70
102) 24+(-43)=-19
103) -91+37=54
104) 52-38=14
105) -11-97=108
106) -5+(-3)=-8
107) -6-9=-15
108) -24+36=12
109) 14+(-6)=9
110) 1-12=-11
111) -15+4=-11
112) 8-20=-12
113) 18-20=-2
114) -24-(-10)=-34
115) 45-(-3)=48
116) -56-14=-70
117) -12+(-3)=-15
118) 17-(-39)=56
119) 46-58=-12
120) -8-(-9)=1
121) 24-21=3
122) -5+(-89)=-94
123) 35-(-5)=40
124) -3,4+(-1)=-4,4
125) -7,5+3=-4,5
126) -2,3+(-6,2)=-8,5
127) 3,5-(+5,8)=-2,3
128) -2,6-3,7 =-6,7
15+12=27 страниц прочитал за среду и четверг вместе
100-27=73 страниц
ответ: 73 страниц книги осталось прочитать Коле.