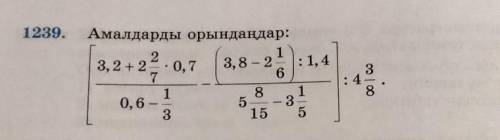
128
Пошаговое объяснение:
Остановимся на этом моменте:
n(n+1)/2=64k
n(n+1)=128k
Заметим, что среди чисел n и n+1 ровно одно четное и одно нечетное! (так как они идут по порядку).
Также 128=2⁷
Это значит, что 128 делится только числа, кратные 2-м (2, 4, 8, 16 и т.д), то есть делится только на четные числа!
Нечетное число никогда нацело не поделится на четное.
Таким образом произведение n(n+1) поделится на 128 только в том случае, если один из множителей будет делится на 128.
То есть n может равняться 128, 256, 512 и т.д
Наименьшее чётное: n=128
1)2целых2/7×0,7=16/7×7/10=16×7/7×10=8/5
2)3,2+8/5=3целых 2/10+8/5=3целых 1/5+8/5=16/5+8/5=24/5
3)0,6-1/3=6/10-1/3=3/5-1/3=9/15-5/15=4/15
4)24/5:4/15=24/5×15/4=18
5)3,8-2целых 1/6=3целых 8/10-13/6=38/10-13/6=19/5-13/6=114/30-65/30=49/30
6)49/30:1,4=49/30:1целую 4/10=49/30×10/14=49/42
7)5целых 8/15-3целых 1/5=83/15-16/5=83/15-48/15=35/15=7/3
8)49/42:7/3=49/42×3/7=7/14=1/2=0,5
9)18-1/2=17целых 1/2=17,5
10)17целых 1/2:4целых 3/8=35/2:35/8=35/2×8/35=4