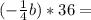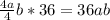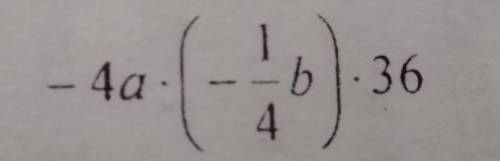
Для правильного решения уравнений нужно уметь пользоваться математическим языком. Словами математического языка являются числовые и буквенные выражения.
Математические выражения могут состоять из одного числа или из одной буквы:
42
z
Или из двух и более чисел и букв, соединённых знаками арифметических действий:
a − 4
2x
x + y
В записи выражений никогда не применяются знаки равенств и неравенств.
= ; ≠ ; > ; < ; ≥ ; ≤
Знаки выше служат для записи равенств и неравенств.
Математические выражения делятся на числовые и буквенные.
Выражение называют числовым, если оно не содержит букв. Примеры числовых выражений:
8
3 · 4
5 : 1
41 + 2 · 3
Если выполнить все действия, содержащиеся в числовом выражении, то получится числовое значение выражения.
Пример:
Запись «30 · 5 + 40» — это числовое выражение.
Выполнив все действия, получим число «190» — числовое значение выражения.
Если какое-либо число в числовом выражении заменить буквой, то полученное выражение называют буквенным.
7t + 5
ab − c
25:5 − y
Читаются буквенные выражения следующим образом.
«4a» − четыре «a»
Более сложные выражения начинают читать по последнему выполняемому действию.
Пошаговое объяснение:
ответ:4
Пошаговое объяснение:
Надо приравнять выражения (3,8 – у)/5,5 и (3,6 – y)/11 и решить получившееся уравнение.
(3,8 – у)/5,5 = (3,6 – y)/11 – применим основное свойство пропорции: В верной пропорции произведение крайних членов пропорции равно произведению средних членов пропорции. Крайние - (3,8 – у) и 11; средние (3,6 – y) и 5,5;
11(3,8 – y) = 5,5(3,6 – y);
41,8 – 11 y = 19,8 – 5,5y – перенесем слагаемые из правой части уравнения в левую с противоположными знаками;
41,8 – 11 y - 19,8 + 5,5y = 0;
- 5,5y + 22 = 0;
- 5,5y = - 22;
y = - 22 : (- 5,5);
y = 4.
Пошаговое объяснение:
-4a