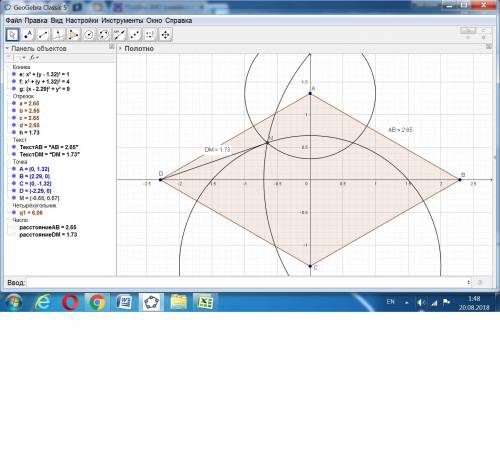
Поместим ромб центром в начало координат.
Точка М лежит на пересечении окружностей с радиусами 1, 2 и 3, центры которых расположены в вершинах равностороннего треугольника АВС.
Координаты точки М(х; у) принадлежат этим окружностям одновременно, то есть, надо составить систему их трёх уравнений окружностей.
Примем половину меньшей диагонали ромба за а, сторона ромба будет 2а, половина большей диагонали а√3.
х² + (у - а)² = 1,
х² + (у + а)² = 4,
(х - а√3)² + у² = 9.
Решение этой системы даёт результат:
а = √7/2, сторона ромба 2а = √7 ≈ 2,645751311 .
Точка М(-√(3/7); (3/2√7) или примерно (-0,654653671; 0,56694671 ).
По разности координат точек М и Д находим длину:
ДМ = √3 ≈ 1,732050808 .
1) 48 984 : 52 = 942
2) 91 375 : 43 = 2 125
3) 243 144 : 72 = 3 377
4) 351 456 : 84 = 4 184