Пошаговое объяснение:
Задача на комбинаторику.
В комбинаторике разделяют два типа задач: на сочетания и размещения.
Сочетание - это тип задач в комбинаторике, в которых порядок элементов не важен.
Размещение - это тип задач в комбинаторике, в которых порядок элементов важен.
У нас задача на размещение.
Формула для решения задач на размещения:
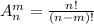
Где n - общее количество карт в колоде; m - количество вальтов; дам.
Подставляем значения в формулу:
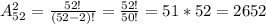
Напоминаю, что 52! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 52.
Следовательно, 50! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 50
52! и 50! можем сократить на 50!, в числителе останется 51 * 52, а в знаменателе - 1(мы числитель и знаменатель всегда можем домножить на единицу).
Получаем
Решаем пункт б:
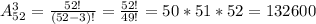
Все то же самое, что и в пункте а.
Задача решена.
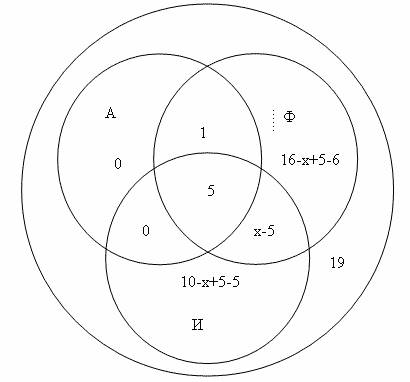
Нам известно, что во всех трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В Франции и Италии нам неизвестно поэтому пишем х-5 в пересечении кругов А и Ф. Т.к. в Англии было 6 человек, то 6-5-1=0 пишем 0,во Франции 16-х+5-6 и Италии 10-х+5-5 и всего в фирме 19 сотрудников, то остается составить и решить уравнение:
1+16-х+5-6+5+х-5+10-х+5-5=19, отсюда х=7, значит в Италии и Франции побывало 7-5=2 сотрудника фирмы
84:14=6(ч)-затратил турист на путь в лагерь
7-6=1(ч)
ответ:На путь в город турист потратил времени больше чем на путь обратно, потому что его скорость на обратном пути была больше чем на пути в город.