Проценты Содержание урока Задание №6 Верных ответов: 2 ВС = 0,9 дм; АС = 2 дм ; Р = 44 дм ВС = 9 см; АС = 20 см; Р = 44 см ВС = 9 см ; АС = 4,05 см; Р = 28,05 см ВС = 90 мм; АС = 200 мм; Р = 440 мм
1) ΔABC прямоугольный AB, BC катеты, Sосн=1/2*AB*BC
2) Высота пирамиды "h", опущенная из вершины D, в точку "0", причем "0" является точкой центром описанной окружности ΔАВС, то есть, точкой пересечения срединных перпендикуляров, проведенных к сторонам ΔАВС.(в часном случае ΔАВС прямоугольный, и "О" лежит на гипотенузе АС )
Δ ΔОЕВ - прямоугольный , с катетами "ОЕ" "ОМ" и дпины их равны половине соответствующих катетов ΔАВС OB²=OE²+OM²=1/4(AB²+BC²)
Из ΔDBO Прямоугольный, известен катет и прилежащий угол,
-мы знаем,что у него денег не осталось,значит после перехода в 3 раз у него было 24 рубля -до перехода у него было 12 рублей(12*2=24) -после того как он перешел мост 2 раз у него стало 24+12=36 -это означает что до перехода было 36/2=18 -после того как он перешел мост 1 раз у него стало 24+18=42 -что означает что до перехода у него было 42/2=21 ответ:у него был 21 рубль. извини перевела в рубли мне так легче уравнением: Пусть у бездельника было Х рублей. Тогда после первого перехода через мост у него стало 2х рублей, да ещё черт отнял 24. Итог после первого перехода 2х - 24 рублей После второго перехода стало 2 * (2х - 24) - 24 = 4х - 48 - 24 = 4х - 72 После третьего перехода стало 2 *(4х - 72) - 24 = 0 8х - 144 - 24 = 0 8х = 168 х = 21 ответ: 21 рубль Проверка: было 21 1 раз перешёл через мост - стало 42 отдал 24 - осталось 18 2 раз перешёл через мост - стало 36 отдал 24 - осталось 12 3 раз перешёл через мост - стало 24 отдал 24 - осталось 0
Пошаговое объяснение:
ДАНО: ПИРАМИДА
ΔАВС- прямоугольный
АВ=15, ВС=15√3
∠a =arctg(2√3)/225
НАЙТИ: Vпирамиды
V= 1/3 Sосн*h
1) ΔABC прямоугольный AB, BC катеты, Sосн=1/2*AB*BC
2) Высота пирамиды "h", опущенная из вершины D, в точку "0", причем "0" является точкой центром описанной окружности ΔАВС, то есть, точкой пересечения срединных перпендикуляров, проведенных к сторонам ΔАВС.(в часном случае ΔАВС прямоугольный, и "О" лежит на гипотенузе АС )
Δ ΔОЕВ - прямоугольный , с катетами "ОЕ" "ОМ" и дпины их равны половине соответствующих катетов ΔАВС OB²=OE²+OM²=1/4(AB²+BC²)
Из ΔDBO Прямоугольный, известен катет и прилежащий угол,
∠a нам дан. tg∠a= OE/OB OE=OB/tg∠a
рабочая формула будет иметь вид
V=1/3 *1/2*AB*BC* h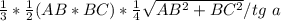
как то так
калькулятор в