Пусть скорость течения Х км/ч, тогда скорость по течению (70+Х) км/ч,
а против течения (70-Х) км/ч.
Значит за 13 часов по течению он Х) км,
а за 15 часов против течения 15(70-Х) км.
По условию задачи известно, что по течению и против течения, он проходил одно и то же расстояние, следовательно эти два выражения можно приравнять, т. е. составляем ур-е:
13(70+Х)=15(70-Х) раскроем скобки
13*70+15Х=15*70-13Х
15Х+13Х=15*70-13*70
28Х=70*(15-13)
28Х=70*2
Х=140:28
Х=5
ответ: скорость течения 5 км/ч
х (км/ч) - скорость течения реки
(20 - х) км/ч - скорость катера против течения
(20 + х) км/ч - скорость катера по течению
Тогда время, затраченное на путь против течения равен:
36/(20 - x) ч
А время пути по течению реки:
22/(20 + x) ч
Составим уравнение:
36/(20 - x) + 22/(20 + x) = 3
36/(20 - x) + 22/(20 + x) - 3 = 0 x ≠ 20, x ≠ - 20
720 + 36x + 440 - 22x - 3 * (20² - x²) = 0
1 160 + 14x - 1 200 + 3x² = 0
3x² + 14x - 40 = 0
D = 14² - 4 * 3 * (- 40) = 196 - (- 480) = 676
= 
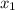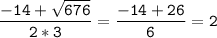км/ч
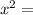
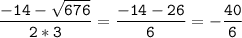- не подходит под условие
ответ: скорость течения реки равна 2 км/ч.
х² + 4х - 12 ≥ 0.
х² + 4х - 12 = 0
D= 4² - 4 · 1 · (-12) = 16 + 48 = 64; √64 = 8
х₁ = (-4 - 8)/2 = -6
х₂ = (-4 + 8)/2 = 2
х² + 4х - 12 = (х + 6)(х - 2)
(х + 6)(х - 2) ≥ 0
+ - +
||
-6 2
x ∈ (-∞; -6] ∪ [2; + ∞) - область определения данной функции