45° и 135°
Пошаговое объяснение:
Для начала вспомним, что такое смежные углы и их "функции". Смежные углы это два и более углов, у которых есть общие стороны (более точное определение все же прочитайте в учебнике, я уже не помню(, а также они по определению вместе составляют 180°. На основе этой информации мы можем составить уравнение, например:
1 угол x° (так как при составлении уравнения важно обозначить наименьшее значение; в качестве наименьшего значения и корня самого уравнения возьмем 1-ый угол)
2 угол (x+90)° (по условию задачи нам известно, что 2-ой угол больше 1-ого на 90°)
Составим уравнение на основе определения смежных углов и решим его:
x + ( x + 90 ) = 180 (так как мы знаем, что в сумме они все равно составят 180°)
2x + 90 = 180
2x = 180 - 90
2x = 90
x = 45
Следовательно 1-ый угол равен 45°, а 2-ой равен 45+90=135°
Для проверки сложите значение первого и второго угла, получается 180, значит задача решена верно
10 см² и 5 см²
Пошаговое объяснение:
Рисунок во вложении
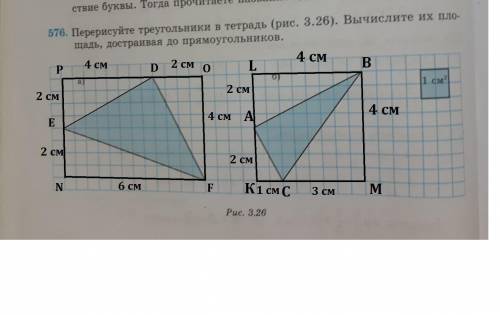
Рис . а
Построим прямоугольник NPOF, который проходит через вершины треугольника EDF.Получили три прямоугольных треугольника EPD,DOF и ENF. Чтобы узнать площадь треугольника EDF(S) надо от площади прямоугольника NPOF(S1) отнять площади треугольников EPD(S2),DOF(S3) и ENF(S4) .Формула площади прямоугольника S=a*b, а формула площади прямоугольного треугольника S=(a*b)/2, где а и b - катеты.
S1=4*6=24 см²
S2=(2*4)/2=4 cм²
S3=(2*4)/2=4 cм²
S4=(2*6)/2=6 cм²
S=S1-S2-S3-S4
S=24-4-4-6=10 см²
Рис.б
Построим прямоугольник КLBM, который проходит через вершины треугольника CAB.Получили три прямоугольных треугольника CKA,ALB и BMC. Чтобы узнать площадь треугольника CAB(S) надо от площади прямоугольника KLBM(S1) отнять площади треугольников CKA(S2),ALB(S3) и BMC(S4) .Формула площади прямоугольника S=a*b, а формула площади прямоугольного треугольника S=(a*b)/2, где а и b - катеты.
S1=4*4=16 см²
S2=(2*1)/2=1 cм²
S3=(2*4)/2=4 cм²
S4=(4*3)/2=6 cм²
S=S1-S2-S3-S4
S=16-1-4-6=5 см²
Средняя линия равна: (71-14-17)/2=20