Полное решение в прикрепленном файле, здесь некоторые подробные расчеты пропущены, так как слишком длинное решение не хочет добавляться.
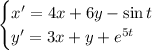
Продифференцируем первое уравнение:
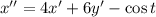
Подставим выражение для y' из второго уравнения:
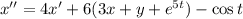
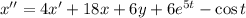
От получившегося уравнения отнимем первое уравнение системы:
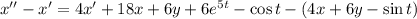
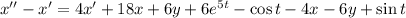
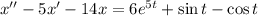
Решим однородное уравнение, соответствующее данному неоднородному:
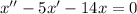
Составим характеристическое уравнение:
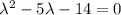
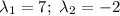
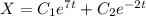
Предположим, что 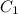 и
и 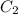 не константы, а некоторые функции
не константы, а некоторые функции 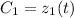 и
и 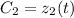 .
.
Найдем первую производную:
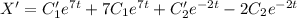
Пусть 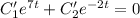 . Тогда:
. Тогда:
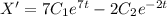
Найдем вторую производную:
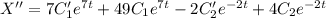
Подставим значения функции и производных в уравнение относительно х:
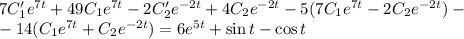
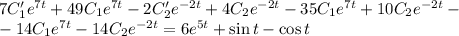
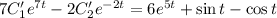
Добавим к полученному уравнению условие, заданное на этапе нахождения первое производной:
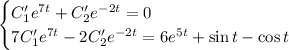
Из первого уравнения выразим 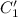 :
:
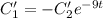
Подставим во второе уравнение:
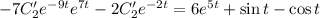
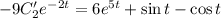
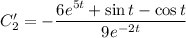
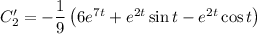
Найдем 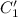 :
:
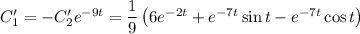
Необходимо проинтегрировать выражения для 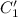 и
и 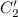 . Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
. Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
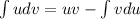
1)
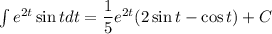
2)
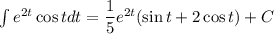
3)
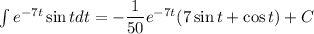
4)
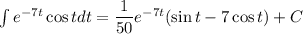
Интегрируем выражение для 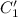 :
:
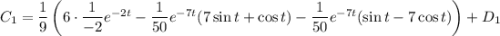
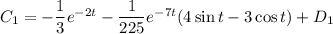
Интегрируем выражение для 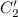 :
:
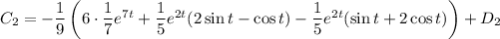
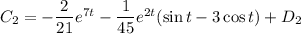
Подставляем выражения для 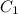 и
и 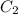 в решение:
в решение:
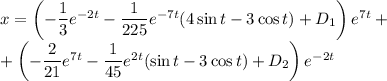
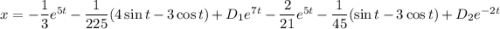
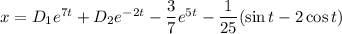
Найдем производную:
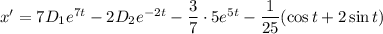
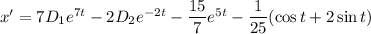
Из первого уравнения исходной системы выразим у:
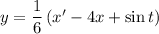
Подставляем выражения для х и х':
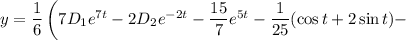
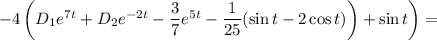
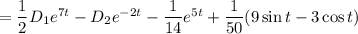
ответ: 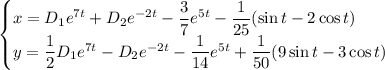
1) длина площадки=16м
ширина площадки=11м
2) 3 упаковки
Пошаговое объяснение:
1) Пусть ширина площадки (а)=х, тогда длина площадки (b)=х+5.
Зная, что площадь прямоугольника вычисляется по формуле S=ab, составим уравнение, подставляя значения выше:
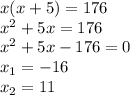
Т.к. наши величины не могут быть отрицательными, делаем вывод, что х = -16 - ложное решение, отсюда следует, что наш х=11.
а=х=11 м - ширина площадки
b=х+5=11+5=16 м - длина площадки
2) Чтобы найти количество упаковок бордюра, нужно знать периметр площадки. Периметр-это сумма всех сторон прямоугольника. Отсюда следует, что периметр прямоугольника равен 11+11+16+16=54 м
Зная, что в одной упаковке находится 25 м бордюра, рассчитаем количество упаковок
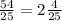 т.к. количество получилось не целым, берем целое число, к которому стремится дробь, т.е 3
т.к. количество получилось не целым, берем целое число, к которому стремится дробь, т.е 3
Чтобы построить бордюр на площадке, потребуется 3 упаковки.
На 25%
Пошаговое объяснение: