Пошаговое объяснение:
№1. 1) первый мастер за 1 час выполнит 1/12 часть работы
второй за 1 час выполнит 1/15 часть работы
1/12 + 1/15 = 5/60 + 4/60 = 9/60 = 3/20 - часть работы выполненная двумя мастерами за 1 час
2) вся работа = 1,
1 : 3/20 = 6 2/3 часа - оба мастера выполнят всю работу, т.е. 100%
3) составим пропорцию: 6 2/3 : 100% = х : 15%, где х - время на 15%,
х = 6 2/3 · 15 : 100 = 1 час. Значит за 1 час они выполнят только 15% работы.
Т.о. для выполнения более 15% работы необходимо больше времени.
ответ: нет
№2. 12/32 = 3/8, сократили числитель и знаменатель на 4. ответ: В
№3. 4/9 = 8/18 , также 2/3 = 12/18, 1/3 = 6/18 . Получили 6 меньше 8, следовательно 1/3 меньше 4/9
или можно просто 1/3 = 3/9, а 3 меньше 4.
ответ: В
№ 1
Примем объем заказа за 1,
тогда за один час работы первый мастер выполняет 1/12 часть заказа,
а второй мастер - 1/15 часть заказа.
Работая совместно за один час работы мастера выполнят:
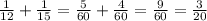 - всего заказа.
- всего заказа.
Весь заказ- 100%.
Найдем процент выполненного заказа за один час совместной работы мастеров:
100% : 20 * 3 = 15%
Значит, не больше 15% заказа мастера выполнят за 1 час совместной работы.
ответ: нет.
№ 2
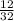
Сократим данную дроб.
Наибольший общий делитель НОД (12; 32) = 4
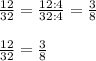
ответ: В 3/8.
№ 4

Приведём данную дробь к знаменателю 18:
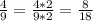
Дроби 17/18 и 11/18 не подходят, так как больше дроби 8/18.
Дроби 1/3 и 2/3 приведём к дробям со знаменателем 9:
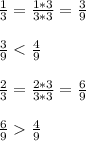
ответ: В 1/3.
Пошаговое объяснение:
чтобы квадратное уравнение ax² + bx + c = 0 имело два разных вещественных корня, необходимо, чтобы дискриминант был больше нуля (D > 0)
D = b² -4ac
наше уравнение перепишем с а₁ чтобы не путать его с "а" из теории
итак
a₁x²- (3a₁+1) x + a₁=0
у нас
а = а₁
b = -(3a₁+1)
c = a₁
найдем дискриминант
D = (-((3a₁+1))² -(4*a₁*a₁) = 9a₁² +6a₁ +1 -4a₁² = 5a₁² +6a₁ +1
и теперь
5a₁² +6a₁ +1 > 0
находим корни (а₁₁ = -1; a₁₂ = -0.2) и смотрим на каком промежутке выполнянтся неравенство. у нас парабола ветвями вверх, значит условие > 0 выполняется при
a₁ ∈ (-∞; -1) ∪ (-0.2; +∞)
ответ
уравнение ax^2- (3a+1) x + a=0 имеет 2 разные корени при
a ∈ (-∞; -1) ∪ (-0.2; +∞)