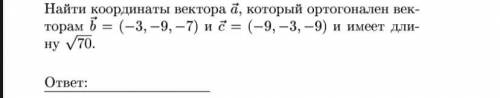
![\vec{a}=(\, x\, ;\, y\, ;\, z\, )\ \ ,\ \ \vec{b}=(-3;-9;-7)\ \ ,\ \ \vec{c}=(-9;-3;-9)\\\\\vec{a}\perp \vec{b}\ \ ,\ \ \vec{a}\perp \vec{c}\ \ \Rightarrow \ \ \vec{a}=\lambda \cdot [\, b\veca}\, \times \, \vec{c}\, ]\\\\\\{}[\ \vec{b}\times \vec{c}\ ]=\left|\begin{array}{ccc}i&j&k\\-3&-9&-7\\-9&-3&-9\end{array}\right|=60\, \vec{i}+36\, \vec{j}-72\, \vec{k}\\\\\\\vec{a}=(\ 60\lambda \, ;\, 36\lambda \, ;\, -72\lambda \, )](/tpl/images/1789/8733/e98e5.png)
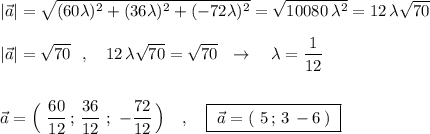
1.15,5
2.17
3.10
Пошаговое объяснение:
1 номер:
1)Достриваем до квадрата ,считаем его площадь
5*5=25
2)Считаем площади прямоугольных треугольников
1)3*3/2=4,5
2)5*2/2=5
3)Вычитаем из площади квадрата площади треугольников
25-4,5-5=15,5
2 номер:
1)Достриваем до квадрата ,считаем его площадь
4*4=16
2)Считаем площади прямоугольных треугольников
1)4*2/2=4
2)4*2/2=4
3)Вычитаем из площади квадрата площади треугольников
25-4-4=17
3 номер:
Достриваем до квадрата ,считаем его площадь
4*4=16
2)Считаем площади прямоугольных треугольников
1)4*1/2=2
2)4*1/2=2
3)2*1/2=1
4)2*1/2=1
5)1*1=1(квадрат)
3)Вычитаем из площади квадрата площади треугольников
16-2-2-1-1=10
Пошаговое объяснение:
В решении таких задач два варианта:
1 - отдельно сложить целые части а дробные привести к наименьшему общему знаменателю, сложить и записать их как дробная часть.
2 - перевести эти дроби в неправильные, привести к общему знаменателю и вернуть его в смешанное число.
РЕШЕНИЕ
1) 3 1/2 + 1 5/6 = 4 + (3+5)/6 4 + 8/6 = 4 + 1 1/3 = 5 1/3 - ответ.
2) 4 2/5 + 9 3/7 = 13 + (2*7 + 3*5)/35 = 13 29/35 - ответ
3) 8 3/4 + 2 7/8 = 10 + (6+7)/8 = 10 + 13/8 = 11 5/8 - ответ
4)2 3/8 + 1 5/6 = (НОЗ=24) = 3 + (3*3 + 5*4)/24 = 3 + 29/24 = 4 5/24 - ответ
5) 6 1/5 + 1 2/3 = (НОЗ=15) = 7 + (1*3+2*5)/15 = 7 13/15 - ответ
6) 4 3/8 + 8 1/2 = 12 + (3 + 1*4)/8 = 12 7/8 - ответ