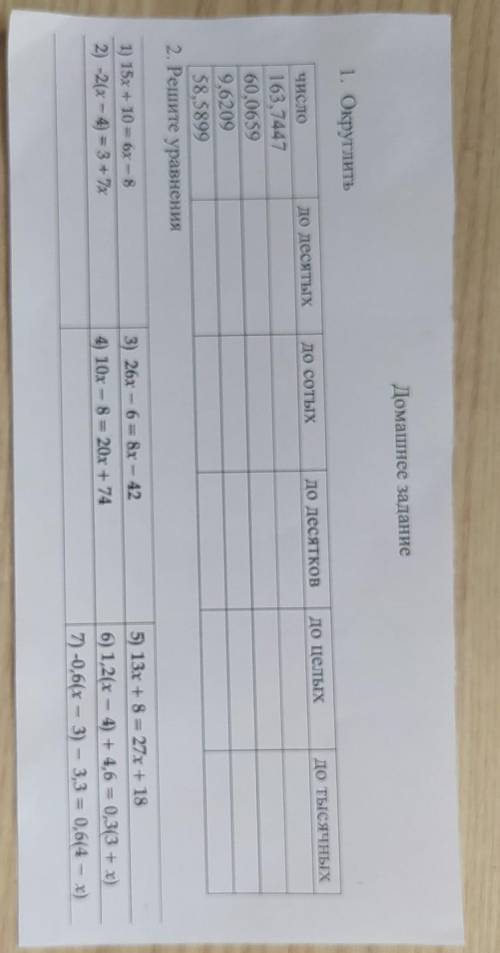
1. 17x-8=20x+7
17x-20x=7+8
-3x=15
x= 15/(-3)
x=-5
2. Решение задачи:
Пусть х – столько килограммов яблок собрал младший брат, тогда 3х кг – собрал старший брат, а (х + 13) кг – собрал средний брат.
По условию задачи вместе три брата собрали 88 кг яблок.
Имеем уравнение:
х + 3х + (х + 13) = 88,
5х + 13 = 88,
5х = 88 – 13,
5х = 75,
х = 75 : 5,
х = 15.
ответ: 15 кг яблок собрал младший брат.
3. не знаю как решать
4. Пусть х л воды было в каждой цистерне первоначально, тогда
(х-54) л воды стало в первой цистерне, а
(х-6) л воды стало во второй цистерне.
Т.К. в первой стало в 4 раза меньше, чем во второй, то составим уравнение: 4(х-54)=х-6, 4х-216-х+6+0; 3х=210; х=70
ответ: в цистернах было по 70л воды
5.Уравнение равняется нулю, когда один из множителей ( в нашем случае выражения в скобках) равен нулю.
Приравняем каждую из скобок к нулю.
(3х+42)(4,8-0,6х)=0
3х + 42 = 0;
3х = - 42;
х = - 42 : 3;
х1 = - 14;
4,8 - 0,6х = 0;
0,6х = 4,8;
х = 4,8 : 0,6;
х2 = 8.
ответ: х1 = - 14 и х2 = 8.
Пошаговое объяснение:
ответ:Пусть х – количество яблок на каждой из веток после сбора.
Тогда первоначально на первой ветке было (х + 3) яблок.
На второй ветке первоначально было (х + х/2) = 1,5х яблок.
А на третьей ветке было (х + 2х) = 3х яблок.
Составим уравнение:
(х + 3) + 1,5х + 3х = 80,
5,5х = 77,
х = 14.
То есть сейчас на каждой из веток по 14 яблок.
Значит первоначально на ветках было:
- на первой ветке (х + 3) = (14 + 3) = 17 яблок,
- на второй ветке 1,5х = 1,5 * 14 = 21 яблоко,
- на третьей ветке 3х = 3 * 14 = 42 яблока.
ответ: на первой ветке первоначально было 17 яблок, на второй ветке было 21 яблоко, а на третьей – 42 яблока.