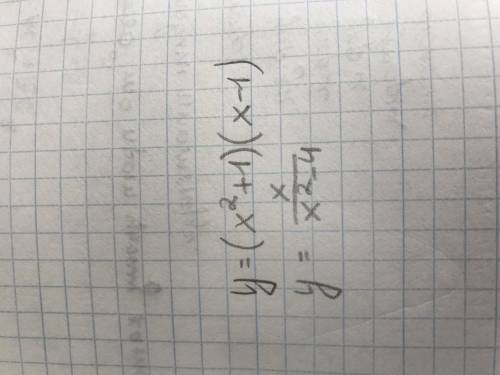
1 Кувшин + 3 кружки + 3 стакана = 2 кувшина + 6 стаканов = 1 кувшин + 4 кружки
Примем:
объем 1 кувшина = V1
объем 1 кружки = V2
объем 1 стакана = V3
Тогда:
Составим три равенства:
(Х) V1+3*V2+3*V3
(Y)2*V1+6*V3
(Z) V1+4*V2
X=Y=Z
V1+3*V2+3*V3=2*V1+6*V3=V1+4*V2
V1+3*V2+3*V3=V1+4*V2
В обоих частях равенства (X и Z) есть одинаковое неизвестное V1 которое можно убрать
Тогда:
3*V2+3*V3=4*V2
Перенесем одинаковые неизвестные
3*V3=4*V2-3*V2
3*V3=V2 - объем трех стаканов равен объему одной кружки
Приравняем оставшуюся часть равенства (Y) и заменим кружку стаканами
2*V1+6*V3=V1+4*V2
2*V1+6*V3=V1+4*3*V3
Перенесем одинаковые неизвестные
2*V1-V1=4*3*V3-6*V3=12*V3-6*V3=6*V3
V1=6*V3 - объем одного кувшина равен объему шести стаканов
В одну кружку вмещается три стакана сока
В один кувшин вмещается шесть стаканов сока
(Используем переместительный закон, чтобы изменить порядок членов. Используя cos(t+s)=cos(t)cos(s)-sin(t)sin(s), записываем выражение в развёрнутом виде) - cos12*cos2*12+sin12*sin2*12/cos(90°+12)=
(Вычисляем значение выражения используя таблицу значений тригонометрических функций или единичную окружность) - 12cos(12)cos(2)+12sin(12)sin(2)/cos(90°)cos(12)-sin(90°)sin(12)=
(Любое выражение, умноженное на 0, равно 0 и любое выражение, умноженное на 1, не изменяется) -
12cos(12)cos(2)+12sin(12)sin(2)/0cos(12)-1sin(12)=
(При добавлении или вычитании 0, величина не меняется) -
12cos(12)cos(2)+12sin(12)sin(2)/0-sin(12)/0-sin(12)=
(Используем -a/b=a/-b=- a/b, чтобы переписать дробь) -
12cos(12)cos(2)+12sin(12)sin(2)/-sin(12)=
- 12cos(12)cos(2)+12sin(12)sin(2)/sin(12)