6 см, 8 см и 10 см.
Пошаговое объяснение:
Пусть один катет будет х см. Тогда второй катет (х+2) см. Периметр треугольника это сумма длин всех сторон. Тогда найдем гипотенузу прямоугольного треугольника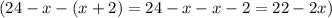 
см. Составим уравнение на основании теоремы Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
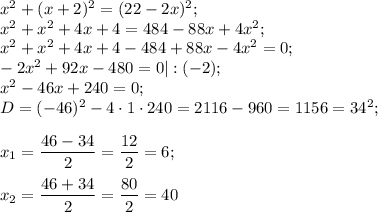
Значит, один катет будет 6 см, второй катет 6+2=8см, а гипотенуза 24-(6+8)=24-14=10 см.
Стороны треугольника 6 см, 8 см и 10 см.
Во втором случае, если один катет 40 см, второй будет 40+2=42 см и тогда периметр меньше, чем каждая из этих сторон и такого треугольника не существует.
Значит, задача имеет одно решение и стороны треугольника 6 см, 8 см и 10 см.
Пошаговое объяснение:
Сторони паралелограма дорівнюють 4.4 см і 5.6 см. Висота проведена до більшої сторони, дорівнює 3,3 см. Обчисліть другу висоту цього паралелограма. Дуже Дякую.
Нехай сторона а = 5.8 см, b = 4.4 см, h_a = 3 см. Знайти h_b.
Знайдемо площу паралелограма:
S = a\cdot h_a\\S = 5.8\cdot 3 = 17.4 \:\: (cm^2)
Використавши формулу ще раз, знайдемо другу висоту:
S = b\cdot h_b \:\Rightarrow \:h_b = \frac{S}{b} \\h_b = \frac{17.4}{4.4} = 3.9 \:\: (cm)
Відповідь: Друга висота паралелограма рівна 3.9 см.
Пошаговое объяснение: