1.Область определения D(x) - х≠0
D(x) - Х∈(-∞;0)∪(0;+∞)
Вертикальная асимптота: Х=0.
2. Пересечение с осью Х. Y=0 - нет.
3. Пересечение с осью У. У(0) - нет (не существует).
4. Поведение на бесконечности.limY(-∞) = + ∞, limY(+∞) = +∞ю
Горизонтальная асимптота - -нет.
5. Исследование на чётность.Y(-x) = - Y(-x).
Функция чётная.
6. Производная функции.Y'(x)= 2*x - 2/x³
Корни при Х1=-1, X2 = 1
7. Локальные экстремумы.
Максимумов - нет. Минимум – Ymin(-1)= Y(min(1) = 2.
8. Интервалы возрастания и убывания.
Возрастает - Х∈(-1;0)∪(1;+∞) , убывает = Х∈(-∞;-1)∪ (0;1).
8. Вторая производная - Y"(x) = 2*(1+3/x⁴)=0.
Корней производной - точек перегиба - нет
9. Вогнутая – «ложка» Х∈(-∞;0)∪(0;+∞) - во всем интервале существования..
10. Область значений Е(у) - У∈(2;+∞)
11. Наклонная асимптота.
Уравнение: lim(oo)(k*x+b – f(x).
k=lim(-∞)(x+1/х³) = +∞. Наклонных асимптот - нет
12. График в приложении.
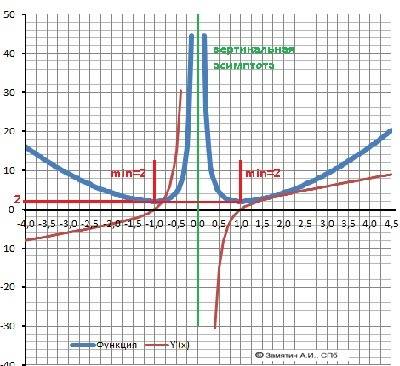
1) Метод разложения на простые множетели:
6 = 3 * 2.
16 = 2 * 2 * 2 * 2.
32 = 2 * 2 * 2 * 2 * 2.
Подчёркнут общий множетель НОД = {2}
НОК находят так, берётся самая длинная цепочка (32-ух)
Это 2 * 2 * 2 * 2 * 2, ищем отличающеися цифры (это 3). Перемножаем 2 * 2 * 2 * 2 * 2 и * 3 = 96 То-есть НОК = {96}
2) Методом перебора
Д (32) = { 1, 32, 2, 16, 4, 8 }
Д (16) = { 1, 16, 2, 8, 4} НОД = { 2 }
Д (6) = { 1, 6, 2, 3}
К (32) = { 32, 48...}
К (16) = { 16, 32, 48...} НОК = { 48 }
К ( 6 ) = { 6, 12, 18, 24, 30, 36, 48...}
27600-20%=22080
Пошаговое объяснение:
смогут