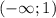Первое число равно 56,25
Второе число равно 11,25
Третье число равно 22,5
Пошаговое объяснение:
Среднее арифметическое трёх чисел равно 30.
Первое число больше третьего числа в 2,5 раз.
Второе число больше третьего в 0,5 раз(-а).
Найди первое, второе и третье число.
Решение.
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на количество слагаемых.
Пусть третье число равно х.
Тогда первое число равно (х * 2,5).
Второе число равно (х * 0,5).
Зная, что среднее арифметическое трёх чисел равно 30, составим уравнение:
((х * 2,5) + (х * 0,5) + х ) : 3 = 30
(2,5х + 0,5х + х) : 3 = 30
4х : 3 = 30
4х = 30 * 3
4х = 90
х = 90 : 4
х = 22,5
Третье число равно 22,5
Первое число равно 22,5 * 2,5 = 56,25
Второе число равно 22,5 * 0,5 = 11,25
Проверка:
(56,25 + 11,25 + 22,5) : 3 = 90 : 3 = 30
Первое число равно 56,25
Второе число равно 11,25
Третье число равно 22,5
a)f(x)=-8x^2-2x+1
f'(x)=-8*2x-2*1=-16x-2
-16x-2>0
-16x>2
x<-2/16
x<-1/8
b)f(x)=1+x-6x^2
f'(x)=1-6*2x=1-12x
1-12x>0
-12x>-1
12x<1
x<1/12
c)f(x)=(x^3/3)-(x^2)+2
f'(x)=1/3 * 3x^2 -2*x=x^2 - 2x
x^2 - 2x>0
x^2 - 2x =0
x(x-2)=0
x=0 x=2
Чертим координатную прямую и отмечаем точки, расставляем знаки.
___+______-______+_____
0 2
Решением неравенства является промежуток
d)f(x)=((-x^3)/3)- 1/2x^2+6/7
f'(x)=-1/3 * 3x^2 - 1/2 * (-2)* 1/x^3 =-x^2 +1/x^3
-x^2 + 1/x^3 >0
Домножим на x^3:
-x^5 +1>0
-x^5>-1
x^5 < 1
x<1
Решением будет являться промежуток