Пошаговое объяснение:
1.) Делители числа 56:
1, 2, 4, 7, 8, 14, 28, 56.
2).НОД (12,32,48)
Наибольший общий делитель чисел 12, 32, 48 - это наибольшее из возможных чисел, на которое делятся все данные числа.
НОД не может быть больше указанных чисел , т.е. 12,32,48.Т.к. 12 наименьшее число, будем на него ориентироваться. Найдем делители числа 12 это 2,3,4,6,12. Проверим делятся ли 48 и 32 на эти числа
48:12=4; 32:12 – не делится
48:6=8 ; 32:6 – не делится
48:4=12; 32:4=8 подходит
Число 48 делится на 4, и число 32 кратно 4. Значит 4 является НОД {12, 32, 48}.
НОД {12, 32, 48} = 4.
3) 2*7*11 и 7*13, наибольший общий делитель будет 7
4) Найдем какие числа будут кратны 15
15*1=15
15*2=30
15*3=45
15*4=60
15*5=75
15*6=90
15*7=105
15*8=120
15*9=135
15*10=150
Ряд будет следующий : 15,30,45,60,75,90,105,120,135,150
5) НОК (4;6;15)
Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
К4 = 4; 8; 12; 16; 20; 24; 28; 32; 36; 40; 44; 48; 52; 56; 60
К6 = 6; 12; 18; 24; 30; 36; 42; 48; 54; 60
К15 = 15; 30; 45; 60
Общее кратное 60
НОК (4,6,15) = 60.
6)НОК 5*7 и 2*7*11
5*7
2*7*11
НОК=5*7*2*11=770
Пошаговое объяснение:
1) i ^ 13 = (i^2)^6 * i = (-1)^6 * i = i
i^100 = (i^2)^50 = (-1)^50 = 1
i^1993 = (i^100)^19 * i^93 = 1 * (i^2)^46 * i = i
2) (1 + i)^10
Воспользуемся формулой Муавра
z^n = r^n(cos φn + i*sin φn)
r - модуль, φ - аргумент комплексного числа
В нашем случае r = √2, φ = 
/4
(1 + i)^10 = (√2)^10 * (cos 10/4 + i*sin 10/4) = 32*(cos 5/2 + i*sin 5/2)=
= 32*(0+i*1) = 32i
Другой вариант решения:
(1 + i)^10 = ( (1 + i)^2 )^5 = (1 - 2i + i^2)^5 = (1 + 2i - 1)^5 = (2i)^5 = 32i * i^4 = 32i
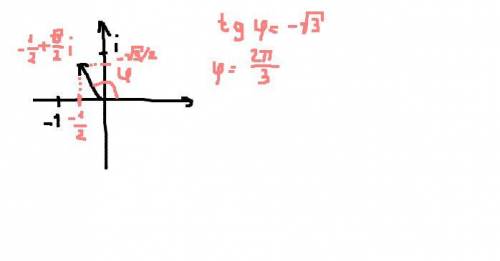
3) a = -1/2 + √3/2 * i
z^n = r^n(cos φn + i*sin φn)
Посчитаем модуль комплексного числа a:
r =√( (-1/2)^2 + (√3/2)^2) = 1
Аргумент φ = 2/3
a^4 = 1^4 * (cos 8/3 + i*sin 8/3) = -1/2 + i*√3/2 = a
a^11 = 1^11 * (cos 22/3 + i*sin 22/3) = -1/2 - i*√3/2
a^1992 = (a^4)^498 = a^498 =
= 1^498 * (cos 498*2/3 + i*sin 498*2/3) = cos 332 + i*sin 332 =
= 1
4) ( (1 + i)/(1 - i) )^1998 = ( (1 + i)^2 / 1^2 - i^2 )^1998 = ((1 + i)^2 / 2)^1998 =
= ((1^2 + 2i + i^2)/2)^1998 = ((1 +2i - 1)/2)^1998 = i^1998 = (i^2)^999 =
= (-1)^999 = -1
(см. объяснение)
Пошаговое объяснение:
Задание выполнено!