На корабле есть несколько кошек, моряков, котёнок и одноногий капитан. Всего 15 голов и 41 ног. Сколько кошек было на борту?
Размышления:
1) У кошек 4 ноги (лапы), у моряков 2, у котёнка 4, у одноногого капитана 1.
2) У всех вышеперечисленных одна голова (морда).
3) Мы знаем число капитанов и котят, поэтому знаем число их голов и ног (лап).
1) Выбросим капитана и котёнка за борт. Получим 13 голов и 36 ног.
2) Обозначим количество кошек через  , а количество моряков через
, а количество моряков через 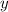 .
.
3) Составим систему уравнений:
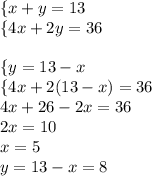
ответ: 5 кошек (и 8 моряков).
P. S. Так и хочется придраться к задаче, что текст составлен немного некорректно: капитан тоже моряк, у кошек нет ног и голов, а есть лапы и морды... Ищешь подвох. Но если следовать такой логике, то задача не решается — я специально проверил.
3 и 12
Пошаговое объяснение:
Количество ребер в полном графе считается по формуле: n(n-1)/2. Где n - количество вершин. (простыми словами, чтобы построить ребро нам нужно 2 вершины; у нас n вариантом для первой вершины и n-1 для второй(можно взять любую кроме взятой первой). Их произведение надо поделить пополам, потому что мы посчитали вариант когда брали сначала вершину А, а потом вершину Б, и вариант когда сначала брали вершину Б, а потом А. Но ребро АБ и ребро БА это одно и тоже ребро. Т.е. мы все ребра посчитали дважды, поэтому и делим на 2.)
Таким образом, если в полном графе G было n вершин, а значит n(n-1)/2=28. Откуда n = 8.
Пусть в полном графе G' было х ребер. Тогда (х + 8)(х + 8 - 1)/2=55. Откуда х = 3.
Аналогично, отвечаем на второй вопрос. Чтобы провести ребро между графом G и графом G', из первого мы можем выбрать любую из 8 вершин, а из второго любую из 3. Их произведение также нужно поделить пополам получим 8*3/2= 12.