Виконайте ділення -5,05:(-5)

Question

Математика: Виконайте ділення -5,05:(-5)

Jubile · Accepted Answer

Пусть первое число а, тогда второе а + d, третье a + 2d. Так как их сумма равна 30, то 3a + 3d = 30. Следовательно, a + d =10. (это второй член арифметической прогрессии). Если первое число оставить без изменения, а от второго и третьего отнять соотвественно 4 и 5, то образуется геометрическая прогрессия: а = 10-d; 10 -4; 10 +d -5 или 10 - d; 6; 5 + d. Используя это условие составим уравнение:

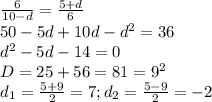
$\frac{6}{10-d}=\frac{5+d}{6}\\50-5d+10d-d^{2}=36\\d^{2}-5d-14=0\\D=25+56=81=9^{2}\\d_{1}=\frac{5+9}{2}=7;d_{2}=\frac{5-9}{2}=-2$

Так как арифметическая прогрессия возрастающая, то подходит только корень уравнения 7. Значит искомые числа: а = 10 - d = 10-7 = 3; 10; 10+7=17.

ответ: 3; 10; 17.

MOGZ ответил

Виконайте ділення
-5,05:(-5)