1) 200 умножить на 3 = 820 - y
600=820-у
у=820-600
у=220
2)в разделить на 6 = 1000 - 220
в разделить на 6 = 978 (умножить обе части уравнения на 6)
в = 5862
Пропорция верна.
Пошаговое объяснение:
1 3/11 : 2/9 = 7,2 : 1 9/35
1)1 3/11 : 2/9 = 14/11•9/2 = 63/11.
2) 7,2 : 1 9/35 = 72/10•35/44 = (72•35)/(10•44) = (18•7)/(2•11) = (9•7)/(1•11) = 63/11.
Видим, что выполнено равенство двух отношений, записанных в правой и левой части, пропорция верна по определению.
Проверим, что в данном равенстве выполнено основное свойство пропорции: произведение крайних членов должно быть равным произведению её средних членов:
1 3/11 : 2/9 = 7,2 : 1 9/35
1 3/11 • 1 9/35 = 2/9•7,2
14/11•44/35 = 2/9•36/5
(14•44)/(11•35) = (2•36)/(9•5)
(2•4)(1•5) = (2•4)/(1•5)
8/5 = 8/5 - верно.
Пропорция верна.
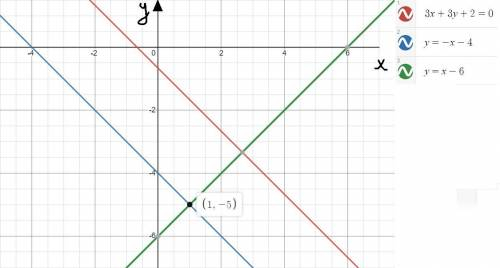
L1: y = -x-4
L2: y = x-6
Пошаговое объяснение:
Дано:
M(1;-5)
L: 3x+3y+2 = 0
Найти: L1, L2
Решение: 1) Для начала выразим прямую L как каноническое уравнение прямой y = kx+b
3x+3y+2 = 0;
3y = -3x-2|:3;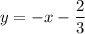
2) Прямые параллельны когда у них меняется свободный член, т.е. k остаётся неизменным, а b нет. Получается коэффициент k у параллельной прямой будет также равен -1
Подставим координаты точки М в каноническое уравнение прямой
-5 = -1*1+b
b = -5+1
b = -4
Уравнение параллельной 3x+3y+2 = 0 прямой, проходящей через точку M(1;-5) будет выглядеть как y = -x-4
3) Для перпендикулярной y = kx+b прямой, проходящей через точку N(x₁,y₁) есть следующая формула:
y-y₁ = -(x-x₁)/k
Получается, перпендикулярная y = -x-²/₃ прямая, проходящая через M(1;-5) будет выглядеть как: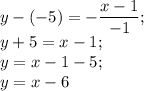
Если построить все данные в одной плоскости, то можно убедиться в правильном нахождении неизвестных прямых(см. вложение)
200 x 3 = 820 - y
600 = 820 - y
y = 820 - 600
y =200