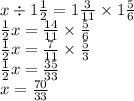
ответ: 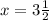
Пошаговое объяснение: лучший ответ и подписку )))
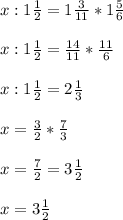
ответ: 1) +∞; 2) 7/3; 3) -5/4; 4) 1/2; 5) e^(-4/3).
Пошаговое объяснение:
1) Подстановка x=∞ приводит к неопределённости ∞/∞. Сокращая числитель и знаменатель дроби на x⁶, получаем lim(x⇒∞) [x⁴+1/x⁴+1/x⁶]/[5+1/x³+2/x⁵]=(∞+0+0)/(5+0+0)=∞/5=∞. ответ: ∞.
2) Подстановка x=1 приводит к неопределённости 0/0. Так как 5*x²-3*x-2=5*(x-1)*(x+2/5), а x³-1=(x-1)*(x²+x+1), то числитель и знаменатель дроби можно сократить на x-1. Тогда данный предел перепишется в виде lim(x⇒1) [5*x+2]/[x²+x+1]=7/3. ответ: 7/3.
3) Подстановка x=1 приводит к неопределённости 0/0. Умножив числитель и знаменатель дроби на √(9-5*x)+2, получим lim(x⇒1) [5-5*x]/[(x-1)*√(9-5*x)+2]=-5*lim(x⇒1) [x-1]/[(x-1)*√(9-5*x)+2]=-5*lim(x⇒1) 1/[√(9-5*x)+2]=-5/(√4+2)=-5/4. ответ: -5/4.
4) Подстановка x=0 приводит к неопределённости 0/0, то есть при x⇒0 числитель и знаменатель представляют собой бесконечно малые величины. Из курса анализа известно, что величина предела не изменится, если входящие в выражение бесконечно малые величины заменить эквивалентными. В данном случае бесконечно малую e^[sin(2*x)]-1 заменим эквивалентной бесконечно малой 2*x, а бесконечно малую arctg(4*x) - эквивалентной бесконечно малой 4*x. Тогда искомый предел запишется в виде lim(x⇒0) [2*x]/[4*x]=1/2. ответ: 1/2.
5) Подстановка x=∞ приводит к неопределённости (∞/∞)^∞. Разделив числитель дроби на знаменатель, получим выражение для предела в виде lim(x⇒∞) [1-2/(3*x+1)]^(2*x+8). Положим 2/(3*x-1)=-t, тогда x=-2/(3*t)-1/3, 2*x+8=-4/(3*t)+22/3 и при x⇒∞ t⇒0. Тогда данный предел запишется в виде lim(t⇒0) [(1+t)^(22/3)/[(1+t)^(4/(3*t))]=1/lim(t⇒0)[(1+t)^(1/t)]^4/3=1/e^(4/3)=e^(-4/3). ответ: e^(-4/3).