3) При возведении обеих частей уравнения в одинаковую четную степень не всегда получаются равносильные уравнения.
Пошаговое объяснение:
1) Утверждение не верно.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня. Например:
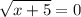
Это уравнение имеет корень х = -5!
2) Утверждение не верно.
Например, если возвести в нулевой степень (0 принадлежит множеству действительных чисел) уравнение, имеющий только корень х=0:
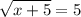
то получим
1 ≡ 1, что означает, последнее верно для любого х∈R.
3) Утверждение верно.
Уравнения называются равносильными, если имеют одно и то же множество корней.
В самом деле, рассмотрим иррациональное уравнение, которое не имеет корней:
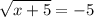
После возведения в квадрат получим:
x+5=25
А это уравнение имеет корень x=20!
Представим, что число состоит из цифр a и b. (a - десятков и b - единиц)
получаем систему уравнений:
a^2+ab = 52
b^2+ab = 117
выразим ab из первого уравнения: ab=52-a^2
подставляем во второе уравнение:
b^2+52-a^2 = 117
b^2-a^2 = 117-52
b^2-a^2 = 65
Поскольку а и b это цифры , составляющие двузначное число, то они целые положительные однозначные числа,
из последнего равенства понятно, что b^2 должно быть больше или равно 65, значит b=9 (т.к. квадрат всех предыдущих цифр меньше 65)
теперь находим a:
81-a^2=65
a^2=81-65
a^2=16
a=4
таким образом искомое число 49