Найти число X для которого верно равенство ×:4\17=34\39

👇

Увидеть ответ

Ответ:

karinakarina9

22.08.2022

8/39

Пошаговое объяснение:

х÷4/17=34/39

х*17/4=34/39

17/4х=34/39 |*4/17

х=8/39.

4,6(10 оценок)

Ответ:

FoxyPixel

22.08.2022

Х:4/17=34/39

Если мы делим какое-то число на дробь, то знаменатель и числитель меняются местами и образуется знак умножить

Х*17/4=34/39

Х=17/4:34/39

Опять числитель меняется со знаменателем

Х=4/17*34/39 сокращаем

Х=8/39

4,8(77 оценок)

Открыть все ответы

Ответ:

Strellerts

22.08.2022

Удобнее всего решать графически, т.к. функции стандартные, графики легко нарисовать, особая точность в рисовании графиков не нужна (т.к. требуется найти количество решений, а не их значения).
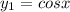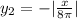Пусть функция слева: $y_{1}=cosx$ , функция справа: $y_{2}=-|\frac{x}{8 \pi}|$ .
Вначале порассуждаем над графиками и свойствами функций.
1) Косинус - периодическая четная функция, период равен 2π.
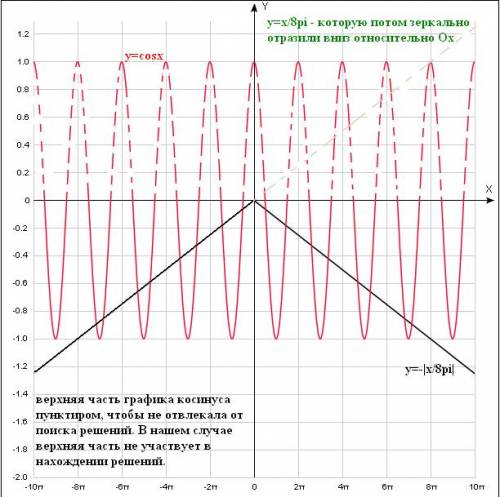
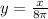2) y2 - это прямая, но за счет модуля "ломаная". Для того, чтобы построить эту функцию, необходимо вначале построить график функции $y= \frac{x}{8 \pi}$ , а затем ту часть, что расположена выше оси Ох, зеркально отобразить вниз (относительно Ох). Получится перевернутая "галочка" с вершиной в точке (0;0).
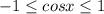3) Теперь найдем интервал, на котором будут пересечения двух графиков. Известно, что $-1 \leq cosx \leq 1$ , значит такие же значения должна принимать и другая функция, т.е.: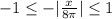 $-1 \leq -|\frac{x}{8 \pi}| \leq 1$
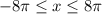
$-8 \pi \leq x \leq 8 \pi$
4) 8π для косинуса - это четыре периода. Значит, вправо от оси Оу будет 4 промежутка возрастания и 4 промежутка убывания. Аналогично влево от оси Оу. Итого: 16 промежутков ("кусочков" функции). Соответственно, прямая пересечет график косинуса в 16 точках.
Убедимся в полученном ответе, начертив графики функций: косинус - стандартная функция, ее общий вид необходимо знать; функция по модулю - уже расписано, как начертить. Оба графика чертим в одной координатной плоскости!

ответ: 16 решений

Найдите количество корней уравнения cosx= - |x/(8pi)| pi - это число пи. это из цт 2014

Найдите количество корней уравнения cosx= - |x/(8pi)| pi - это число пи. это из цт 2014

4,7(30 оценок)

Ответ:

clever113

22.08.2022

4x²-y²=(2x-y)(2x+y)
Решаем уравнение в целых числах:
(2х-у)(2х+у)=3
Слева произведение двух целых чисел (2х-у) и (2х+у) и справа 1 и 3 или (-1) и (-3)
Перебором устанавливаем, что возможны следующие варианты:
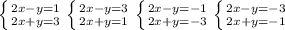
$\left \{ {{2x-y=1} \atop {2x+y=3}} \right. \left \{ {{2x-y=3} \atop {2x+y=1}} \right. \left \{ {{2x-y=-1} \atop {2x+y=-3}} \right. \left \{ {{2x-y=-3} \atop {2x+y=-1}} \right.$
Решаем каждую сложения.
Из первой системы 4х=4, х=1, тогда y=3-2x=3-2=1 ответ (1;1)
Из второй 4х=4, х=1, тогда y=1-2x=1-2=-1 ответ (1:-1)
Из третьей 4х=-4, х=-1, тогда у = -3-2х=-3-2(-1)=-1 ответ (-1:-1)
Из четвертой 4х=-4, х=-1, тогда у=-1-2х=-1+2=1 ответ (-1;1)
ответ. (1;1) (1;-1) (-1;-1) (-1;1)

4,6(22 оценок)

Это интересно:

Дом-и-сад

10.09.2020

Заставьте ваш филодендрон расцвести: советы по уходу за растением...

Взаимоотношения

01.11.2020

Как определить, что девушка пытается увести вашего парня...

Кулинария-и-гостеприимство

22.12.2021

Как приготовить вкусное мороженое из молока в домашних условиях...

Компьютеры-и-электроника