√26sin(α+π/2), если ctgα=-5 , 0°<α<180°. Не могу понять как выбрать знак при косинусе ведь он лежит между 180 и 0
Пошаговое объяснение:
{ctgα=-5 ( котангенс отрицателен во 2и 4 четвертях)
{ 0°<α<180° ( это 1 и 2 четверти)
Из этих двух условий следует , что α∈ II четверти. Во 2 четверти cosα<0.
√26sin(α+π/2)= √26cosα
Т.к 1+ctg²α=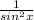 , то 1+(-5)²=
, то 1+(-5)²= , sin²α=1/26.
, sin²α=1/26.
По основному тригонометрическому тождеству
sin²α+cos²α=1
1/26+cos²α=1
cos²α=1-1/26
cos²α=25/26
cosα= -√(25/26) , cosα= -5/√26.
√26sin(α+π/2)= √26cosα= √26*(-5/√26)= -5
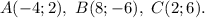
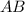 это уравнение прямой, проходящей через точки
это уравнение прямой, проходящей через точки 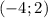 и
и 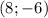 . Исходя из этого составим систему уравнений:
. Исходя из этого составим систему уравнений: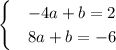
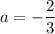 и
и 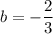 . Получили, что сторона
. Получили, что сторона 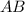 задаётся уравнением
задаётся уравнением 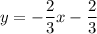 .
.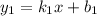 и
и 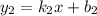 будут перпендикулярны, если
будут перпендикулярны, если 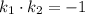 , коэффициенты
, коэффициенты 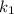 и
и 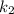 называются угловыми коэффициентами.
называются угловыми коэффициентами. 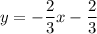 . Тогда
. Тогда 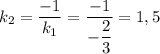 , где
, где 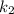 - это угловой коэффициент прямой
- это угловой коэффициент прямой 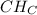 . Получаем, что эту прямую можно записать в виде
. Получаем, что эту прямую можно записать в виде 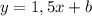 . Теперь, зная, что эта прямая проходит через точку
. Теперь, зная, что эта прямая проходит через точку 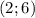 , найдём
, найдём 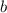 :
: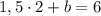 , откуда
, откуда 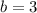 . Получается, что высота
. Получается, что высота 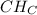 задаётся уравнением
задаётся уравнением 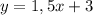 .
.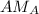 делит отрезок
делит отрезок 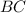 пополам. Вычислим координаты середины отрезка
пополам. Вычислим координаты середины отрезка 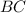 , т.е. точку пересечения медианы со стороной
, т.е. точку пересечения медианы со стороной 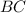 :
: 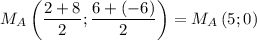 .
.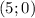 и
и 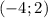 . Найдём её уравнение по этим данным:
. Найдём её уравнение по этим данным: 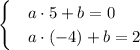
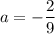 и
и 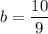 .
.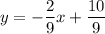 .
.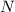 медианы
медианы 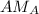 и высоты
и высоты 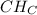 найдём, решив соответствующую систему уравнений:
найдём, решив соответствующую систему уравнений: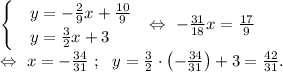
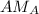 и высота
и высота 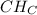 пересекаются в точке
пересекаются в точке 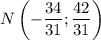 .
.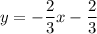 , выглядит следующим образом:
, выглядит следующим образом: 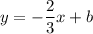 . Нам нужно, чтобы эта параллельная прямая проходила через точку
. Нам нужно, чтобы эта параллельная прямая проходила через точку 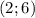 .
.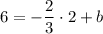 , откуда
, откуда 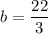 .
. 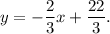
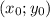 до прямой
до прямой 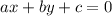 вычисляется по формуле
вычисляется по формуле 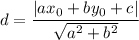 . Нам нужно расстояние от точки
. Нам нужно расстояние от точки 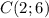 до прямой
до прямой 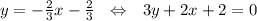 .
. 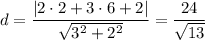 .
.
100-70=30
105\30Х100