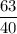 Пошаговое объяснение:Нарисуем сначала нашу область D.1) y = x
Пошаговое объяснение:Нарисуем сначала нашу область D.1) y = xЭто прямая, которая проходит через начало координат и находится под углом в 45 градусов от полуоси Ох, проходит например через точку (1 1)
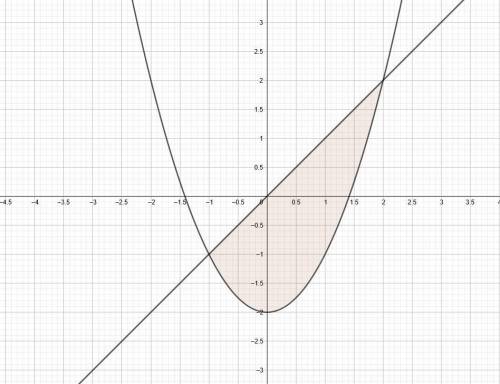
2) y = x² - 2Это парабола (перед нами квадратный трехчлен) Вершина в точке (0 2), образована путем смещения всех точек параболы у = х² на 2 единицы вниз
Смотрите вложение!
Мы интегрируем по красной области1) Запишем границых меняется от -1 до 2 это границы, х координаты точек пересечения (видно из графика)
Для того, чтобы из найти решим уравнение
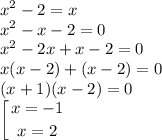
Это будут первые границы по х
Границы по у - это функции от х. Снизу (нижняя граница) функция 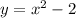 а верхняя граница функция
а верхняя граница функция 
Тогда запишем двойной интеграл как пару интегралов, зная границы
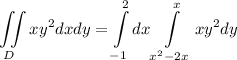
Решим данный интеграл
1 Проинтегрируем 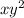 по у
по у
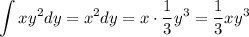
константу не пишу специально, так как сейчас буду писать пределы
2 Вычислим
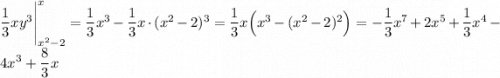
3 Проинтегрируем полученную функцию по х
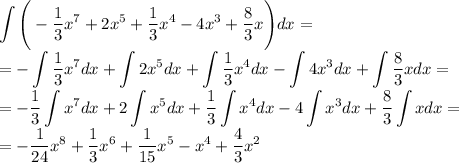
4 Подставляем пределы и считаем

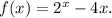 Её производная
Её производная 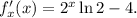 Найдём её ноли.
Найдём её ноли.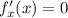 ;
; ;
;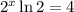 ;
;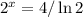 ;
;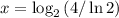 ;
;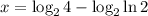 ;
;![x = 2 - \frac{ \ln{ \ln{2} } }{ \ln{2} } \approx 2 - [-0.528766] = 2.528766](/tpl/images/0486/4136/ee6c4.png) ;
; например при
например при 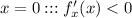 ;
; например при
например при 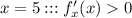 ;
;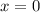 функция
функция 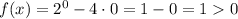 ;
;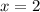 функция
функция 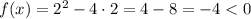 ;
;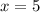 функция
функция 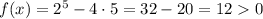 ;
;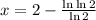 функция
функция 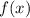 строго убывает, причём переходя от положительных при
строго убывает, причём переходя от положительных при 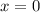 значений к отрицательным, а значит имеет до указанной точки ровно один корень. А далее от точки
значений к отрицательным, а значит имеет до указанной точки ровно один корень. А далее от точки 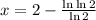 функция
функция 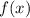 строго возрастает, причём переходя от отрицательных значений к положительным при
строго возрастает, причём переходя от отрицательных значений к положительным при 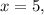 а значит, имеет после указанной точки ровно ещё один корень.
а значит, имеет после указанной точки ровно ещё один корень.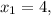 заявленный и в приведённом условии. Далее порассуждаем практически:
заявленный и в приведённом условии. Далее порассуждаем практически: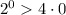 ;
;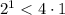 ;
;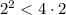 ;
;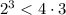 ;
;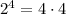 ;
;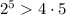 ;
;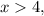 производная
производная 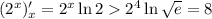 больше производной
больше производной 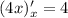 , т.е. дальше левая часть уравнения, растёт быстрее, чем правая, а значит, других корней при
, т.е. дальше левая часть уравнения, растёт быстрее, чем правая, а значит, других корней при 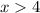 быть не может.
быть не может.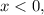 левая часть уравнения положительна, а правая отрицательна, так что других корней при
левая часть уравнения положительна, а правая отрицательна, так что других корней при 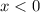 быть не может.
быть не может.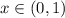 , так как при сравнении двух непрерывных функций на этом интервале меняется знак.
, так как при сравнении двух непрерывных функций на этом интервале меняется знак.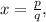 где
где 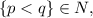 то:
то: ![2^x = 2^\frac{p}{q} = (\sqrt[q]2)^p < 2 .](/tpl/images/0486/4136/dd2eb.png) Это число, очевидно иррационально, что легко доказать от обратного методом Евклида. Однако справа должно быть рациональное число
Это число, очевидно иррационально, что легко доказать от обратного методом Евклида. Однако справа должно быть рациональное число 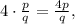 а значит, мы пришли к противоречию. Таким образом, второе решение иррационально.
а значит, мы пришли к противоречию. Таким образом, второе решение иррационально.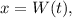 по определению дающая решение, т.е. являющаяся обратной, к функции
по определению дающая решение, т.е. являющаяся обратной, к функции 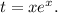 Функция вводится аналогично, скажем, функции
Функция вводится аналогично, скажем, функции 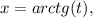 являющейся решением уравнения
являющейся решением уравнения 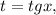 но в отличие от арктангенса, функция Ламберта используется намного реже в прикладных задачах (в основном в задачах теплопроводности), и поэтому – менее широко известна. Функция вводится на расширенной комплексной плоскости, т.е. алгебраически, а не арифметически, а значит по определению, может быть многозначной, и является таковой при отрицательных значениях аргумента
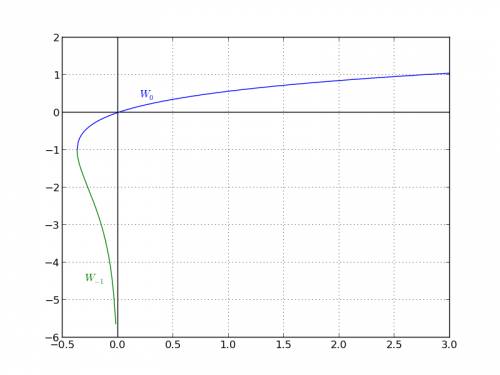
но в отличие от арктангенса, функция Ламберта используется намного реже в прикладных задачах (в основном в задачах теплопроводности), и поэтому – менее широко известна. Функция вводится на расширенной комплексной плоскости, т.е. алгебраически, а не арифметически, а значит по определению, может быть многозначной, и является таковой при отрицательных значениях аргумента 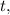 хотя нам достаточно будет знать лишь её действительные значения, которых при отрицательных аргументах всегда два. Вид действительных ветвей функции Ламберта представлен на приложенном изображении.
хотя нам достаточно будет знать лишь её действительные значения, которых при отрицательных аргументах всегда два. Вид действительных ветвей функции Ламберта представлен на приложенном изображении.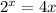 ;
;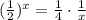 ;
;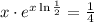 ;
;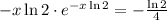 ;
;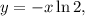 тогда:
тогда: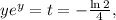 отсюда через функцию Ламберта:
отсюда через функцию Ламберта: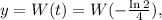
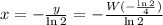 ;
;
ответ: 0,27
27% = 0,27