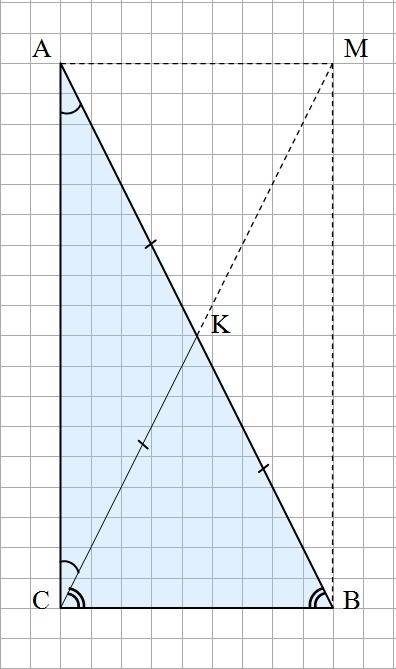
1). Строим произвольный прямоугольный треугольник АСВ. ∠АСВ = 90°.
В этом треугольнике - два острых угла: ∠САВ и ∠СВА.
Докажем, что сумма ∠САВ + ∠СВА = 90°.
2). Достраиваем треугольник АСВ до прямоугольника АМВС.
Диагонали прямоугольника равны и делятся точкой пересечения пополам. Тогда: АК = КВ = СК и СК - медиана ΔСАВ, проведенная к гипотенузе.
Образовались два равнобедренных треугольника: ΔАКС и ΔСКВ.
В ΔАКС: АК = СК => ∠КСА = ∠САК. (1)
В ΔСКВ: СК = КВ => ∠КСВ = ∠КВС. (2)
Так как в ΔАСВ прямой угол ∠АСВ = ∠КСА + ∠КСВ = 90°.
Учитывая (1) и (2), получим: ∠АСВ = ∠САК + ∠КВС = 90°.
Что и требовалось доказать.
НОД (Наибольший общий делитель) 126 и 132
Наибольший общий делитель (НОД) двух данных чисел 126 и 132 — это наибольшее число, на которое оба числа 126 и 132 делятся без остатка.
НОД (126; 132) = 6.
Как найти наибольший общий делитель для 126 и 132
Разложим на простые множители 126
126 = 2 • 3 • 3 • 7
Разложим на простые множители 132
132 = 2 • 2 • 3 • 11
Выберем одинаковые простые множители в обоих числах.
2 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (126; 132) = 2 • 3 = 6
НОК (Наименьшее общее кратное) 126 и 132
Наименьшим общим кратным (НОК) 126 и 132 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (126 и 132).
НОК (126, 132) = 2772
Как найти наименьшее общее кратное для 126 и 132
Разложим на простые множители 126
126 = 2 • 3 • 3 • 7
Разложим на простые множители 132
132 = 2 • 2 • 3 • 11
Выберем в разложении меньшего числа (126) множители, которые не вошли в разложение
3 , 7
Добавим эти множители в разложение бóльшего числа
2 , 2 , 3 , 11 , 3 , 7
Полученное произведение запишем в ответ.
НОК (126, 132) = 2 • 2 • 3 • 11 • 3 • 7 = 2772