Пусть a и b - стороны левого верхнего прямоугольника, тогда b и c - стороны правого верхнего прямоугольника, c и d - стороны правого нижнего прямоугольника, b и d - левого нижнего прямоугольника. Тогда: Р₁=2(a+b)=24 Р₂=2(a+c)=28 Р₃=2(c+d)=16 Р₄=2(b+d) - ? Отнимем третий периметр от второго. Получим: P₂₃=Р₂-Р₃=28-16=12 С другой стороны: P₂₃=Р₂-Р₃=2(a+c)-2(c+d)=2(a+c-c-d)=2(a-d) Значит, 2(a-d)=12 Теперь отнимем полученное от первого периметра: Р₁-P₂₃=24-12=12 С другой стороны: Р₁-P₂₃=2(a+b)-2(a-d)=2(a+b-a+d)=2(b+d) Значит, 2(b+d)=12, что и требовалось найти.
Пошаговое объяснение:
Выясним, при каких значениях переменной функция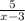 не определена.
не определена.
R ( x ) =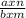 , где n - степень числителя, а m - степень знаменателя.
, где n - степень числителя, а m - степень знаменателя.
Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
Если n = m , то горизонтальной асимптотой является прямая y = a b .
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m .
n = 0
m = 1
n < m , ось X, y = 0 , является горизонтальной асимптотой. y = 0
Вертикальные асимптоты: x = 3
Горизонтальные асимптоты: y = 0
Нет наклонных асимптот.