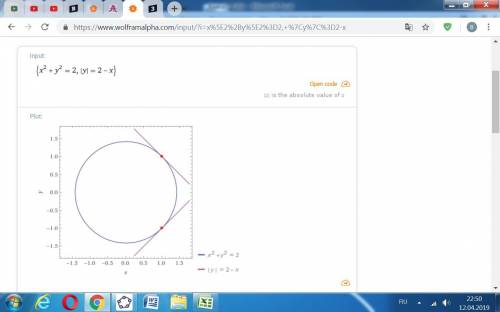
Заданная система уравнений х^2 + у^2 = 2, х+|y| = a графически представляет собой 3 фигуры:
- окружность х^2 + у^2 = 2,
- прямую у = -х + а,
- прямую у = х - а.
Эти прямые взаимно перпендикулярны и чтобы было 2 решения, они должны касаться окружности каждая в одной точке.
Радиусы в точку касания параллельны прямым, но так как они идут из начала координат, то их уравнения у = х и у = -х.
Возьмём у = х и у = -х + а и приравняем: 2х = а, х =а/2, но и у = х = а/2.
Подставим ув уравнение окружности: (а²/4) + (а²/4) = 2, 2а² = 8,
а² = 8/2 = 4. Отсюда а = +-2.
ответ: наибольшее значение параметра а равно 2.
НОД 72 ; 60 =12 , НОК 72;60 =360
Пошаговое объяснение:
НОД:
нужно разложить числа на простые множители
72=2*2*2*3*3
60=2*2*3*5
находим одинаковые простые множители и перемножаем их, получаем НОД(наибольший общий делитель) - 2*2*3=12
НОД 72 и 60 является 12
НОК:
в первой строке раскладываем на множители большее число то есть -72, а за тем меньшее -60
72=2*2*2*3*3
60=2*2*3*5
Те множители, которые не вошли в разложении большего числа, мы добавляем к большему, в нашем случае 5, затем все перемножаем.
2*2*2*3*3*5 = 360
НОК 72 и 60 является 360
2) в числителе 31х (90-35) = 31 х 55
в знаменателе 35 х 31
далее 31 сокращается, а 55 и 35 сокращается на 5, получается 11/7 или 1 4/7
1) в знаменателе 9Х0,3= 2,7 получается 2,7 х 3,9
сокращаем 2,7 получаем 7,8 / 3,9 сокращаем на 2 получаем 2