А тупоугольный треугольник - уже не треугольник?)
Углы можно уменьшать. Например, синус120 - это косинус30. Вот и свелось к углу попроще.
Тригонометрия - не только треугольники. Просто с них все началось. Точно также сперва придумали числа натуральные, потом 0, потом целые, потом дробные и в конце концов иррациональные. "Где можно использовать иррациональные числа" - спросили люди древности))) Более того, за всякие разговоры о такой природе вещей в те времена можно было и жизни лишиться. Сейчас же об этих числах знает любой. Но я отвлекся.
Угол имеет свойство повториться после 360 градусов. Поэтому люди проверили, как будет себя вести тригонометрия, если попробовать пихнуть в функцию не обычный угол до 90, а что-то другое, ну и получили обобщение на любой угол, так как основные тригонометрические вещи цикличны. Зачем? Потому что это возникает в задачах. Да и просто прикольно. Математика вегда все обобщает. Люди придумывают нечто, с надеждой, что кому-то пригодится это обобщение. Ну а если уж о практике - синусы да косинусы, да и в целом тригонометрия - не только
углы и геометрия в школе. Например, синусом описываются волны (они и зовутся синусоидами) из мобилки, с монитора, волны от огня на плите, от обогревателя, от микроволновки... звуковые, в конце концов. Стоит ли говорить о практическом применении волн? Кручение колеса в машине, прогибание кровати под моим весом, колебание струнки в гитаре, или вот - качественный звук в плеере - это вообще интеграл от синуса с косинусом... Продолжать можно вечно, а о тысячах применений я и не знаю. Все что в мире циклично, все что колеблется - все тригонометризуется)) По части чистой математики - это вещи, которые дали возможность решить многие теоретические задачи. Более того, тригонометрия является связующим звеном многих, казалось бы, совершенно разных разделов математики. Она повляла на жизнь многих разделов математики, которые нашли свое применение в сложной физике, и сейчас люди использя эти знания, которые базируются в том числе на тригонометрии, пытаются находить ответы на самые темнве загадки природы. Это настолько фундаментальная вещь, что она просто везде, куда не ткни.
Тригонометрия используется в невообразимо большом количестве математических работ, которые позволяют воплощать в жизни вещи, которые мы используем в повседневности. Очень многие вещи которые с тригонометрией не связаны - связаны с другими вещами, которые связаны еще с чем-то, что где-то там далеко использует тригонометрию. Точно также незаметно, как я не замечаю присутствие математики когда пишу весь этот текст сюда.
Не стоит задавать вопрос "зачем мне это надо здесь и сейчас". Ибо ответ прост: незачем. Вам в жизни скорее всего нужно будет умение считать, например сдачу, да и все тут. Но стоит помнить, что каждую секунду вы используете сотни и тысячи трудов различных математиков, физиков и тд. Каждое мгновение на вас работают миллионы часов работы ученых. И я вам больше скажу, эти труды работают на вас сейчас, а не на них - тогда. Это был безвозмездный труд на будущее, задумайтесь об этом.
Зачем же они это сделали? Решите сами :]
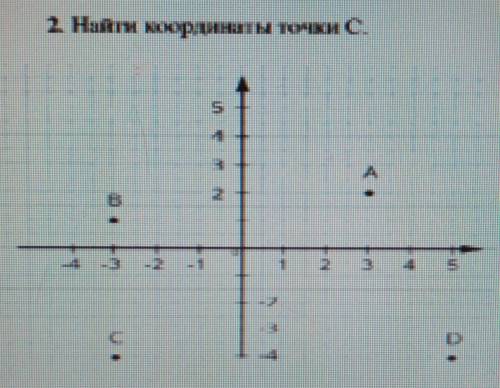
С.
х=-3; у=-4
Пошаговое объяснение: