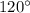По поводу первой. Если отбросить тех, кто "забронировал билеты", то останется 11 билетов на 11 человек. Теперь нам нужно отобрать 7 человек на нижнюю полку или 4 человека на верхнюю. Это $C_{11}^7 = C_{11}^4=330$
По поводу второй. Учитываем решение первой, но берем во внимание, что порядок должен быть учтен размещения 5 человек по 5 местам размещения 4 человек по 4 местам - $A_4^4=4!$. С учетом правила произведения - $C_{11}^7\cdot 4!\cdot 5! = C_{11}^4\cdot 4!\cdot 5!=950400$
Пошаговое объяснение:
Извини если не правильно.
Здравствуй,
1)
Т.к. все спички одинаковой длины, то берём три спички и строим из них треугольник
(
), он будет равносторонним, а, как известно, в равностороннем треугольнике все углы равны 
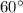
2)
Ну, здесь можно взять 4 спички и построить квадрат (
), каждый из его 4 углов будет равен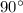 
...
3)
Ну, а здесь можно построить из 5 спичек два треугольника с одной общей стороной, потом же, спичку, которая является общей стороной для этих двух треугольников можно убрать, а те два угла, которые эта спичка соединяла будут равны