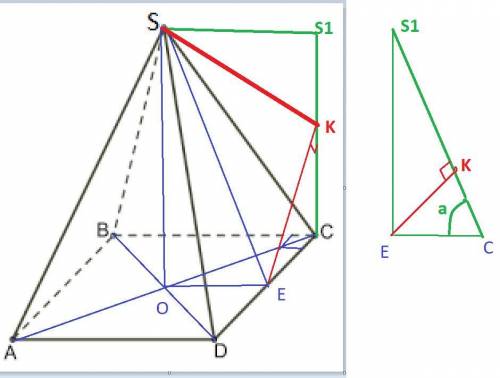
Пусть дана правильная четырехугольная пирамида SABCD.
В боковой грани проведена апофема SE.
Рассмотрим проекцию SE на смежную грань BCS.
Точка S остаётся на месте, а вот точку Е надо проецировать на плоскость BCS.
Надо продлить плоскость BCS до перпендикулярной к ней плоскости, проходящей через ребро CD, в котором находится основание апофемы точка Е.
Приведен рисунок со схемой такого проецирования.
Для конкретных условий необходимы данные по пирамиде - длина ребра основания и угол наклона боковой грани к основанию.
Или же другие данные, определяющие пирамиду.
1) Фигура, принадлежащая пересечению множеств А и В - это фигура, обладающая одновременно свойствами множества А и множества В. Такими свойствами обладает прямоугольный равнобедренный треугольник. (см. вложение)
2) Если А – множество однозначных чисел, В – множество нечётных натуральных чисел, меньших 19, то объединение этих множеств - множество, в котором находятся все однозначные числа и нечетные натуральные числа, меньшие 19.
A={0,1,2,3,4,5,6,7,8,9}
B={1,3,5,7,9,11,13,15,17,}
А∪В={1,2,3,4,5,6,7,8,9,11,13,15,17}
3) см. вложение.


№3 : на 1 %
№5: цифрой 8