![\begin{cases} [x]+\{y\}=-2.13\\ [y]+\{x\}=3.5\end{cases}](/tpl/images/4863/6648/56f50.png)
Отметим области значений для функции целой и дробной части:
![y=[x];\ E(y)=\mathbb{Z}](/tpl/images/4863/6648/a9281.png)
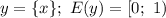
Выразим из первого уравнения целую часть числа "х":
![[x]=-2.13-\{y\}](/tpl/images/4863/6648/256e6.png)
Зная оценку для дробной части числа, оценим правую часть:
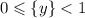
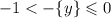
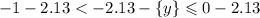
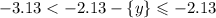
Так как правая часть равна левой, то можем переписать:
![-3.13 < [x]\leqslant-2.13](/tpl/images/4863/6648/f07c8.png)
Но ![[x]](/tpl/images/4863/6648/6e538.png)
- это целое число. Единственное целое число, подпадающее в промежуток ![(-3.13;\ -2.13]](/tpl/images/4863/6648/d99d0.png)
- это число -3.
Таким образом:
![[x]=-3](/tpl/images/4863/6648/2938f.png)
Тогда, выражая второе неизвестное из первого уравнения, получим:
![\{y\}=-2.13-[x]](/tpl/images/4863/6648/1b2bc.png)
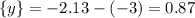
Аналогичные действия проделаем со вторым уравнением. Сначала выразим целую часть числа "у":
![[y]=3.5-\{x\}](/tpl/images/4863/6648/08246.png)
Оценим правую часть:
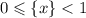
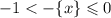
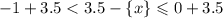
Так как правая часть равна левой, то:
![2.5 < [y]\leqslant3.5](/tpl/images/4863/6648/b44ed.png)
Единственное целое число, подпадающее в промежуток ![(2.5;\ 3.5]](/tpl/images/4863/6648/43585.png)
- это число 3:
![[y]=3](/tpl/images/4863/6648/64ca9.png)
Выражаем второе неизвестное из второго уравнения:
![\{x\}=3.5-[y]](/tpl/images/4863/6648/008ca.png)
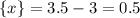
Остается найти сами числа "х" и "у". Для этого представим их в виде суммы своих целой и дробной частей:
![x=[x]+\{x\}=-3+0.5=-2.5](/tpl/images/4863/6648/21c23.png)
![y=[y]+\{y\}=3+0.87=3.87](/tpl/images/4863/6648/78e06.png)
ответ: (-2.5; 3.87)
2) Варианты длины и ширины: 6 и 4; 7 и 3; 8 и 2; 9 и 1.
При площади в 24кв.см подходит вариант 6 и 4. Длина = 6см; ширина = 4см.
6 * 4 = 24(кв.см) - площадь
3) 22 : 2 = 11(см) - полупериметр, или сумма длины и ширины
При площади 24кв.см подходит вариант: длина 8см; ширина 3см
8 * 3 = 24(кв.см) - площадь
Надо начертить:
1-ый прямоугольник с размерами: длина 6см; ширина 4см
2-ой прямоугольник с размерами: длина 8см; ширина 3см.