Рассмотрим максимальное число победных игр: 75 : 3 = 25 (игр), но при таком варианте игр вничью быть не может.
Будем уменьшать число победных игр и считать, сколько за это команда получит очков. Предположим, что победных игр 24: 24 · 3 = 72. Таким образом, в данной конфигурации может быть 24 победы, 3 поражения и 3 ничьи.
Предположим, что победных игр 23: 23 · 3 = 69. Получаем, что 6 очков за ничью и 0 очков за поражение.
Предположим, что победных игр 22: 22 · 3 = 66. Получаем, что такой ситуации быть не может, так как максимальное число игр вничью — восемь, следовательно, 8 очков — 66 + 8 = 74, а в условии сказано, что команда набрала 75 очков.
Таким образом, наибольшее число ничейных матчей — 6.
Признак делимости на 6: число делится на 6, если сумма всех цифр этого числа делится на 3 и последняя цифра этого числа делится на 2.
Значит последней цифрой может стоять только 0, так как 1; 3; 5;7 - нечетные числа .
Остается составить двузначные числа из цифр 1; 3; 5; 7, при условии, что каждая цифра встречается в числе только 1 раз:
4!/(4!-2!)=
4!/2!=
4*3*2*1/2*1=
4*3=12
Можно составить 12 двузначных чисел:
31 35 37
51 53 57
71 73 75
Теперь нужно найти числа, подходящие для составления 3-х значных чисел, по условию задания. Это могут быть числа, сумма цифр которых делится на 6:
15; 51; 57;75
С правой стороны ставим 0 и получаем 3-х значные числа. которые делятся на 6
150; 510; 570; 750
ответ: Можно составить 4 числа
ответ: 3 числа
Пошаговое объяснение:
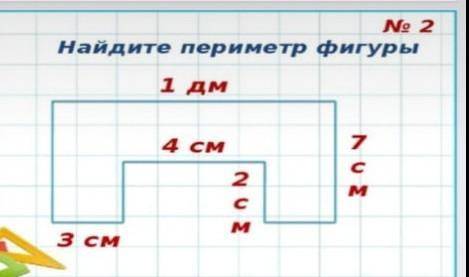
Периметр равен : 10 +7*2+4+3*2+2*2= 38 см