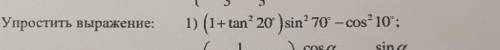
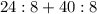
повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение:
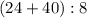
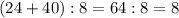В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на , то и их сумма делится на .
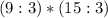
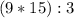
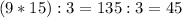
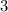,то их произведение делится на 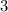" доказанным.
Пошаговое объяснение:
(tan20)^2=sinx^2/cosx^2
поэтому мы можем написать (1+ sinx^2/cosx^2) после этого мы имеем (1×cosx^2+sinx^2)/cosx^2
как мы знаем cos^2+sin^2 равен одному
1/cosx^2 × sin 70^2 - cos10^2
мы синус 70 в квадрате можем преобразить как cos 20^2 потому есть такая формула sin(π/2-x)=cosx
1/cosx^2 × cosx^2 равен 1
и у нас остается 1 -cos10°^2 а это по формуле равен sin10°^2
1-sin^2=cos^2 и наоборот