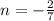 - знаменатель обращается в 0.
- знаменатель обращается в 0.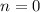 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)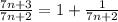

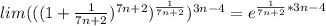 (при
(при  →∞)
→∞)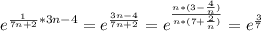 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→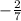
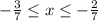 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
var b,i,z,k: integer;
a: array[1..10000] of integer;
begin
read(b);
z: =0;
k: =0;
while b> 0 do
begin
z: =z+1;
a[z]: = b mod 10;
b: =b div 10;
end;
for i: =2 to z-1 do
if a[i]=a[i-1] or a[i]=a[i+1] then
k: =1;
if k=1 then writeln (‘да’)
else writeln (‘нет’);
end.
второй способ:
var a,b,c: integer;
begin
read(a);
k: =0;
c: =10; // это должно быть обязательно число, но не цифра
while a > 0 do
begin
b: =a mod 10;
a: =a div 10;
if b=c then k: =1;
c: =b;
end;
if k=1 then writeln (‘да’)
else (‘нет’);
end.
2)4*2*2=16 м 1-4дерево
3)4*4*2=32 м5-6деерво
4)7+16+32=55 м всего надо пройти