4)52*x - x*x^2 + 1 + 1 > x + 6
Пошаговое объяснение:
5)1) 2(3x + 1) - x ≤ 3(x + 4), 2) 7x + 4(x - 2) > 6(1 + 3x),
6х + 2 - х ≤ 3х + 12, 7х + 4х - 8 > 6 + 18x,
5х + 2 ≤ 3х + 12, 11x - 8 > 6 + 18x,
5х - 3х ≤ 12 - 2, 11x - 18x > 6 + 8,
2х ≤ 10, -7x > 14,
х ≤ 5, x < - 2,
х ∈ (-∞; 5]; x ∈ (-∞; -2);
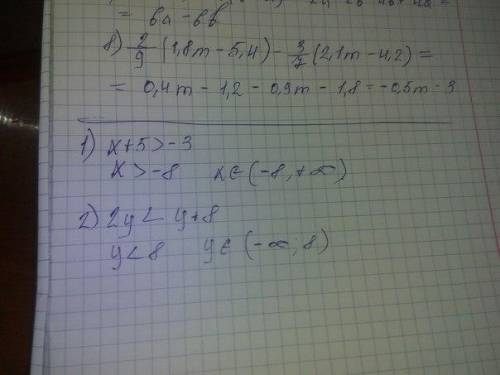
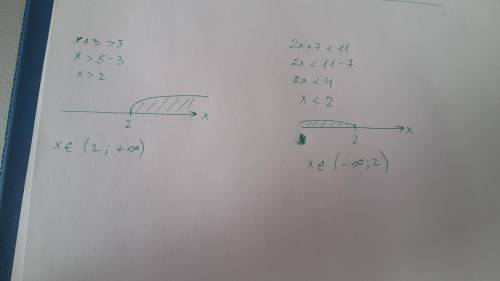
Для того, чтобы узнать сколько существует целых чисел , модуль которых меньше 5, но больше 2, решим в целых числах следующее двойное неравенство:
2 < |x| < 5.
Рассмотрим два случая.
1) х >= 0.
При таких значениях х неравенство 2 < |x| < 5 принимает вид:
2 < x < 5.
Очевидно, что данное неравенство имеет два целочисленных решения:
х = 3 и х = 4.
2) х < 0.
При таких значениях х неравенство 2 < |x| < 5 принимает вид:
2 < -x < 5.
Умножая все части неравенства на -1 и меняя знаки неравенства, получаем:
-5 < x < -2.
Очевидно, что данное неравенство имеет два целочисленных решения:
х = -4 и х = -3.
ответ: существует 4 целых числа, модуль которых меньше 5, но больше 2.
Пошаговое объяснение: