Пошаговое объяснение:
касательная АВ. точка касания В; АО1 = О1В; ∠ ВАС - обозначим ∠α
теперь
АО = ОС (это из того, что ОО1 средняя линия ΔАВС)
ОА = ОС = х; ВС = у
ВС/АС = tg α и поскольку АВ касательная, то это у'
т.е.
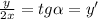
дальше решаем дифференциальное уравнение
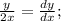
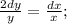 ⇒
⇒ 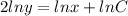 ⇒
⇒ 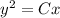
получилась парабола.
если бы была какая-нибудь точка, через которую парабола проходит, то можно было бы написать точное уравнение.
а так ответ такой
отрезок любой касательной, заключенный между точкой касания и осью абсцисс делится осью ординат пополам у параболы
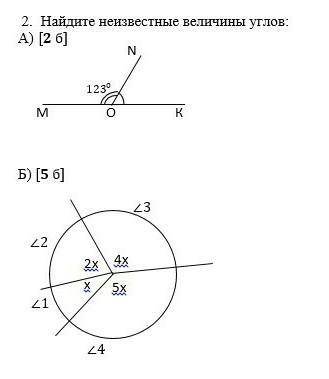
а) ∠NOK = 180° - 123° = 57°
б) 360° = х+2х+4х+5х = 12х
х = 360°/12 = 30
∠1 = 1*30 = 30°
∠2 = 2*30 = 60°
∠3 = 4*30 = 120°
∠4 = 5*30 = 150°