Дано уравнение линии в декартовой системе координат: r= 5/3-4cosf.
Преобразуем уравнение к виду r=p/(1-e*cos(a)).
Здесь r- фокальный параметр, е - эксцентриситет, f - полярный угол.
Числитель и знаменатель дроби разделим на 3.
r=(5/3)/(1-(4/3)*cos(f)).
Так как эксцентриситет е = (4/3), то есть больше 1, то заданная кривая - гипербола.
Перевод в Декартову систему координат.
Радиус r = √(x² + y²), cos f = x/√(x² + y²).
Получаем уравнение √(x² + y²) = 5/(3 - (4x/√(x² + y²))).
Если выразить относительно "у" уравнение, то получим:
y = ±(1/3)*√(7x² + 40x + 25).
В общем виде уравнение: 7x² - 9y² + 40x + 25 = 0.
Выделим полные квадраты:
7(x²+2·(20/7)x + (20/7)²) -7·(20/7)² - 9y² + 25 =
= 7(x+(20/7)²) - (400/7) - 9y² + 25 = 0.
7(x+(20/7)²) - 9y² = 225/7.
Разделим все выражение на (225/7).
Получаем каноническое уравнение гиперболы.
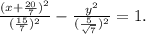
Данное уравнение определяет гиперболу с центром в точке:
C((-20/7); 0) и полуосями: a = (15/7). b = 5/√7.
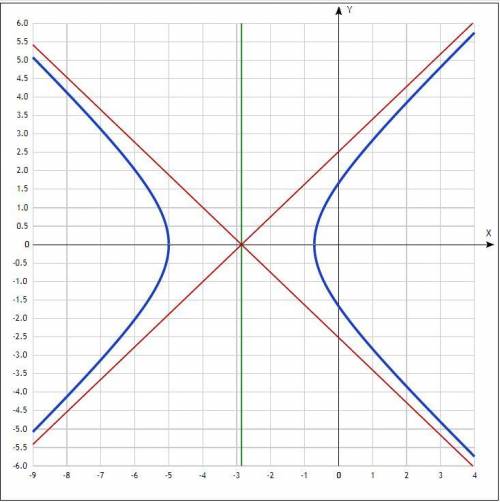
ответ:
пошаговое объяснение:
1)
2x + 17 = 22 + 3x;
3x - 2x = 17 - 22
x = -5
2)
18 + 3x = x+14;
3x - x = 14 - 18
2x = -4
x = -4 : 2
x = -2
3)
25 — 4х = 12 — 5x;
5x - 4x = 12 - 25
x = -13
4)
13х + 27 = 16х + 4,5;
16x - 13x = 27 - 4,5
3x = 22,5
x = 22,5 : 3
x = 7,5
5)
21х + 45 = 17 + 14x;
21x - 14x = 17 - 45
7x = -28
x = -28 : 7
x = -4
6)
13х + 70 = 2х + 15.
13x - 2x = 15 - 70
11x = -55
x = -55 : 11
x = -5
781.
1)
3,4х – 4 = 4,8 – х;
3,4x + x = 4,8 + 4
4,4x = 8,8
x = 8,8 : 4,4
x = 2
2)
2x + 7 = х + 5,5;
2x - x = 5,5 - 7
x = -1,5
3)
5 – 3x = 2х – 8;
2x + 3x = 5 + 8
5x = 13
x = 13 : 5
x = 2,6
4)
9,5х + 2 = 5,7х – 5,6;
9,5x - 5,7x = -5,6 - 2
3,8x = -7,6
x = -7,6 : 3,8
x = -2
5)
1,5х + 8 = 3,1х + 16;
3,1x - 1,5x = 8 - 16
1,6x = -8
x = -8 : 1,6
x = -5
6)
2,9x + 7,4 = x + 1,7.
2,9x - x = 1,7 - 7,4
1,9x = -5,7
x = -5,7 : 1,9
x = -3