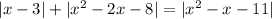
1. Найдем нули модулей
1) 
≈ 
≈ 
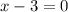
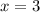
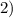
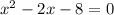
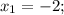
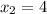
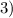
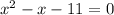
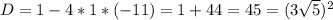
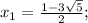
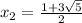
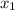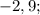
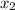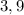
2. Отметим полученные точки на координатной прямой.
__________-2,9____-2_________3_________3,9__4______
Получили 6 числовых промежутков, на каждом из них раскроем модули.
а) На промежутке (-∞; -2,9)
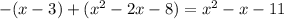
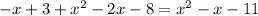
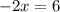
∈ (-∞; -2,9) первый корень х= -3
б) (-2,9; -2]
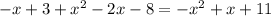
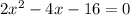
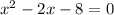
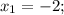∈ (-2,9; -2] второй корень х= -2
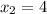∉ (-2,9; -2]
в) [-2; 3]
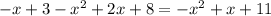
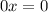
- любое число
г) [3; 3,9]
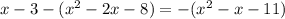
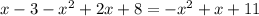
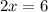
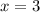∈ [3; 3,9] третий корень х= 3
д) {3,9; 4]
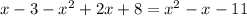
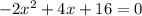
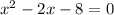
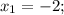∉ {3,9; 4]
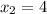∈ {3,9; 4] четвертый корень х= 4
е) [4; +∞]
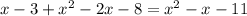
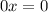
- любое число в том числе и х=0
ответ: {-3; -2; 0; 3; 4}
V(max)=8 .
Пошаговое объяснение:
S(t)=-1/6t³+t²+6t-10
V=S'(t)=(-1/6t³)'+(t²)'+(6t)'+(-10)'=
=-3/6t²+2t+6+0=-0,5t²+2t+6+0=
=-0,5t²+2t+6
Находим точки экстремума:
S'(t)=0
-0,5t²+2t+6=0 | ·(-2)
t²-4t-12=0
D/4=4-(-12)=16=4²>0
t₁=2+4=6
t₂=2-4=-2
Это парабола, ветви направлены вниз.
Точкой максимума является вершина
параболы. Определим координаты вершины.
х₀=-в/2а=-2/2·(-0,5)=-2/-1=2
y₀=-0,5·2²+2·2+6=-2+4+6=8
Точка максимума - это вершина параболы
(2; 8) .
V(max)=8
Скорость достигает максимального значения
в момент времени t=2 .