777 литра
Пошаговое объяснение:
Пусть в 1-сосуде Х литр воды, а во 2-сосуде 0 литр воды.
1-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 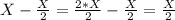
2-сосуд: 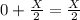
Объем воды в обоих сосудах в сумме дают Х литр!
2-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 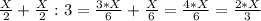
2-сосуд: 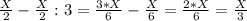
Объем воды в обоих сосудах в сумме дают Х литр!
3-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 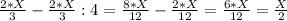
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
Теперь покажем, что в нечётных числах переливания всегда
1-сосуд: 
2-сосуд: 
Пусть n=2·k+1.
n-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 
2-сосуд: 
(n+1)-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 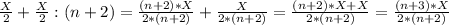
2-сосуд: 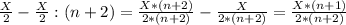
(n+2)-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 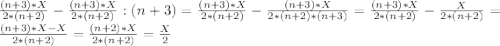
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
что требовалось показать.
Отсюда, 2019 - нечётное и X=1554 литра, тогда
1-сосуд: 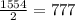
Вот то, что нам известно:
xyx - число
2x+y=13
yxx=xyx+360
Делаем методом подбора. Так как цифра единиц и сотен совпадает, то их сумма должна делиться на 2 без остатка:
13=0+13
13=2+11
13=4+9
13=6+7
13=8+5
13=10+3
13=12+1
Нолик убираем, так как число трёхзначное (он был лишь для того, чтобы указать все числа, которые делятся на 2). Числа 13 и 11 выбывают тоже, так как на месте десятков должна быть лишь одна цифра.
Теперь пробуем составить числа из оставшегося:
13=4+9; число - 292
13=6+7; число - 373
13=8+5; число - 454
13=10+3; число - 535
13=12+1; число - 616
Теперь пытаемся применить эти числа ко второму условию (yxx=xyx+360):
1. 922=292+630
2. 733=373+360 (подходит)
3. 544=454+90
355 и 166 меньше своих изначальных значений, тут сложение даже не пройдёт :))
ответ: это число 373.