
Рисунок во вложении.
1. Нарисовать две прямые а и b.
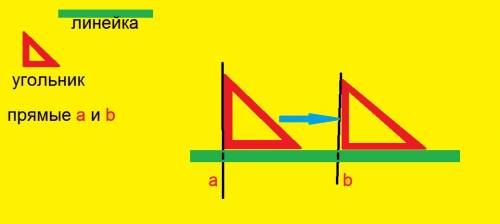
2. Совместить сторону (катет) прямого угла угольника с прямой а, а к другой стороне (катету) приложить линейку.
3. Двигать угольник по линейке до прямой b.
4. Проверить, если та сторона, которая была совмещена с прямой а, совмещается, также, и с прямой b.
Если совмещается, то прямые параллельны, если нет - то не параллельны.
На рисунке видно, что сторона угольника не совместилась с прямой b, значит эти прямые не параллельны.
ответ: построение параллельных прямых неточное, a ∦ b.
При данной проверке подтвеждается правило параллельности прямых: " Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны."
В роли третьей прямой выступает линейка, а угольник проверяет, если углы пересечения прямых а и b с линейкой равны.
Чтобы найти НОД нескольких чисел, нужно разложить эти числа на множители и найти произведение их СОВМЕСТНЫХ множителей, взятых с НАИМЕНЬШИМ показателем степени.
38 = 2 * 19
48 = (2*2*2*2) * 3
102 = 2 * 3 * 17
НОД (38, 48,102) = 2 - наибольший общий делитель
50 = 2 * (5*5)
75 = 3 * (5*5)
250 = 2 * (5*5*5)
НОД (50,75,250) = (5*5) = 25 - наибольший общий делитель
44 = (2*2) * 11
110 = 2 * 5 * 11
154 = 2 * 7 * 11
НОД (44, 110, 154) = 2 * 11 = 22 - наибольший общий делитель
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Чтобы найти НОК нескольких чисел, нужно разложить эти числа на множители и найти произведение ВСЕХ множителей, взятых с НАИБОЛЬШИМ показателем степени.
60 = (2*2) * 3 * 5
24 = (2*2*2) * 3
36 = (2*2) * (3*3)
НОК (60, 24, 36) = (2*2*2) * (3*3) * 5 = 360 - наименьшее общее кратное
36 = (2*2) * (3*3)
90 = 2 * (3*3) * 5
200 = (2*2*2) * (5*5)
НОК (36, 90, 200) = (2*2*2) * (3*3) * (5*5) = 1800 - наименьшее общее кратное
90 = 2 * (3*3) * 5
60 = (2*2) * 3 * 5
135 = (3*3*3) * 5
НОК (90, 60, 135) = (2*2) * (3*3*3) * 5 = 540 - наименьшее общее кратное
Пошаговое объяснение: