
Углы треугольника равны ∠A = 53°, ∠В = 78°, ∠С = 49°.
Пошаговое объяснение: рисунок к задаче в прикрепленном файле
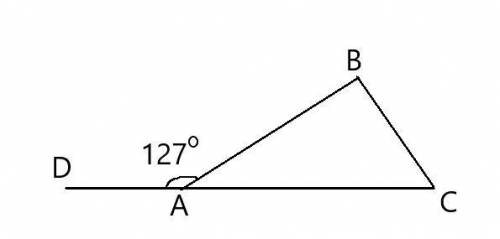
ДАНО:
Δ АВС
∠DAB = 127°
∠B - ∠C = 29°
НАЙТИ: ∠А - ?, ∠В - ?, ∠С - ?
Свойство смежных углов: сумма смежных углов равна 180°.
Угол А является смежным с углом DAB, значит,
∠A = 180° - ∠DAB = 180° - 127° = 53°
Теорема о внешнем угле треугольника: внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с этим внешним углом.
Исходя из теоремы ∠DAB = ∠B + ∠C = 127°.
Из условия ∠B - ∠C = 29°, выразим угол В через угол С:
∠В = 29° + ∠С ,
и подставим в полученное выше равенство
29° + ∠С + ∠C = 127°
29° + 2∠С = 127°
2∠С = 127° - 29°
2∠С = 98°
∠С = 98° : 2
∠С = 49°
Найдем угол В :
∠В = 29° + 49° = 78°.
H = D*sin 60° = 12*(√3/2) = 6√3 см.
d = D*cos 60° = 12*0,5 = 6 см.
Сторона основы призмы равна половине d:
a = d/2 = 6/2 = 3 см.
Площадь основы (шестиугольника) равна:
So = 3√3a²/2 = 3√3*9 /2 = 27√3/2 см².
Объём призмы V = So*H = (27√3/2)*6√3 = 243 см³.