на плоскости:
1) пролегает мимо окружности
2) пролегает через центр окружности
3) прямая имеет 2 точки касания с окружностью
4) прямая имеет 1 точку касания с окружностью
в мимо окружности в перпендикулярной плоскости
6) мимо окружности под углом к плоскости окружности
7) пролегает через центр окружности в перпендикулярной плоскости
8) пролегает через центр окружности под углом к плоскости окружности
9) прямая имеет 1 точку касания с окружностью в перпендикулярной плоскости
10) прямая имеет 1 точку касания с окружностью под углом к плоскости окружности
11) прямая имеет 1 точку касания с кругом в перпендикулярной плоскости
12) прямая имеет 1 точку касания с кругом под углом к плоскости окружности
Пошаговое объяснение:
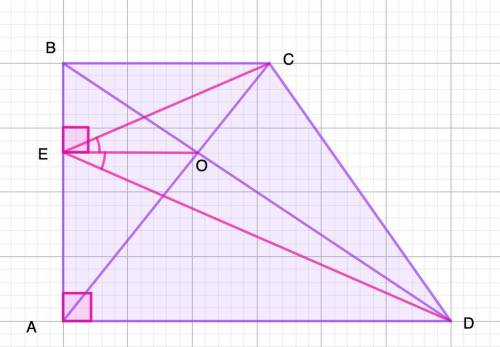
Дано: ABCD - прямоугольная трапеция
ОЕ⊥АВ
Доказать: ∠СЕО=∠DEO
Доказательство:
1. CB⊥AB; AD⊥AB; OE⊥AB ⇒CB║AD║OE
2. Рассмотрим ΔABD и ΔЕВО
OE║AD
⇒ ΔABD ~ ΔЕВО (лемма о подобных треугольниках)
Составим пропорцию:
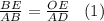
3. Рассмотрим ΔABС и ΔАЕО
OE║ВС
⇒ ΔABС ~ ΔАЕО (лемма о подобных треугольниках)
Составим пропорцию:
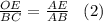
4. Выразим из (2) ОЕ и подставим в (1):
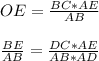
Отсюда получим:
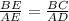
5. Рассмотрим ΔЕВС и ΔAED - прямоугольные.
∠А=∠В=90°
Стороны пропорциональны (п.4):
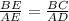
⇒ ΔЕВС ~ ΔAED
⇒∠BEC=∠AED
6.
∠CEO=90°-∠BEC
∠DEO=90°-∠AED
⇒∠CEO=∠DEO