b=0,8
Пошаговое объяснение:
подставляем в уравнение
2*3+b*(-6)-1,2 =0
6-6*b-1,2=0
4,8-6*b=0
6*b=4,8
b=0,8
x€[-2; 16]
Пошаговое объяснение:
1) Преобразовать десятичную дробь в обыкнавенную то есть:
0,8х преобразуем в 4/5.
2)Дальше 0,48 преобразем 12/25.
3)Записать все числители над знаминателем.
3) Упростить составную дробь
4) умножить обе части неравенства на 50.
5)Умножить 2 на скобку
6) привести подобные челены.
7)Делаем расстановку:
Все числа в левую часть а простые числа в правую с изменением знака.
8)Сложить числа
9)Разделить неравенство -17 и поменять знак неравенства.
И нижний пример тоже самое только числа поменялись.
Пошаговое объяснение:
1) рисуем графики и находим пределы интегрирования по х 0<x<1
при замене переменных поменяются и пределы интегрирования
![\displaystyle S=\int\limits^1_0 {\frac{x}{(x^2+1)^2} } \, dx =\left[\begin{array}{ccc}u=x^2+1\hfill\\du=2xdx\hfill\\u_1=1\quad u_2=2\end{array}\right] =\frac{1}{2} \int\limits^2_1 {\frac{1}{u^2} } \, du =-\frac{1}{2u} \bigg |_1^2=\frac{1}{4}](/tpl/images/1760/1934/9ff6a.png)
2) это уравнение эллипса с полуосями 9 и 4
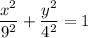
рисуем график и находим нужную область
теперь находим пределы интегрирования
у = 2 4sint = 2 sint = 0.5 t = π/6
y= 4 4sint = 4 sint = 1 t =π/2
здесь заметим, что параметрические уравнения «прорисовывают» дугу эллипса «в противоход» оси х , а площадь фигуры считается слева направо. поэтому нижнему пределу интегрирования соответствует значение π/2, а верхнему пределу – значение π/6
поэтому мы для вычисления интеграла поменяем знак интеграла на - и пределы "перевернем"
это будет половина нужной нам области
по формуле площадей фигур для функции заданной параметрически
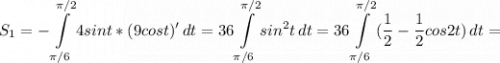
дальше несложная замена переменных u=2t du=2dt с заменой пределов интегрирования u₁=π/3 u₂= π получим
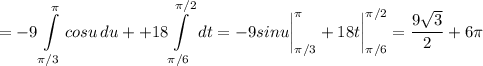
и теперь умножим S₁ на 2 и получим искомую площадь
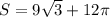
3)
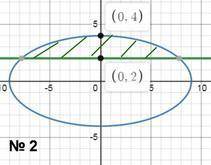
это уравнение "полярной розы" с 12 лепестками
период sin6Ф
6(Ф+T) = 6Ф +6T 6Ф+6T=6Ф+2π
T= 2π/6 = π/3
тогда у нашей розы 6 одинаковых секторов (в каждом по 2 одинаковых лепестка)
сектор одного лепестка от 0 до π/6
по формуле площади криволинейного сектора рассчитем площадь одного лепестка и умножим ее на 12
![\displaystyle S_c=\int\limits^{\pi /3}_0 {sin^26\phi} \, d\phi=\left[\begin{array}{ccc}u=6\phi\\du=6d\phi\\u_1=0 \quad u_2=\pi \end{array}\right] =\frac{1}{12}\int\limits^\pi _0 {sin^2u} \, du =](/tpl/images/1760/1934/43459.png)
после несложных замен переменных и пределов интегрирования (s=2u ds=2du s₁ =0 s₂=2π) получим
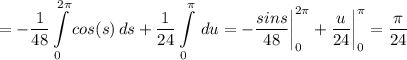
и полная площадь
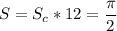

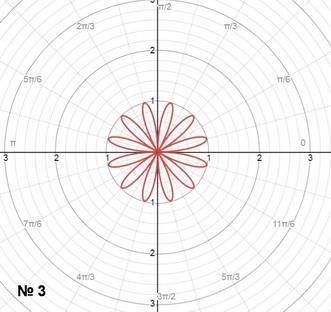
2*3-6b-1,2=0
6-6b-1,2=0
4,8-6b=0
-6b=-4,8
b=0,8
Пошаговое объяснение: