Постройте график прямой пропорциональности, проходящий через точку А(-6;2). б) Запишите формулу этой прямой пропорциональности. в) Найдите абсциссу точки В(х;9) г) Найдите ординату точки К(-12; у)

, ЭТО СОР!

Question

Математика: Постройте график прямой пропорциональности, проходящий через точку А(-6;2). б) Запишите формулу этой прямой пропорциональности. в) Найдите абсциссу точки В(х;9) г) Найдите ординату точки К(-12; у) , ЭТО СОР!

Dodod616 · Accepted Answer

а+(n-1)d - формула будь-якого члена арифметичної прогресії, де а - перший член арифметичної прогресії, d - різниця прогресії, n- порядковий номер члена прогресії.

Тоді:

а+d - другий член арифметичної прогресії.

а+7d - восьмий.

а+2d, а+3d, а+5d - третій, четвертий і шостий члени відповідно.

а+6d - сьомий.

Відомо, що: (а+7d)-8/(а+d)=2; (а+2d)+(а+3d)+(а+5d)=51

(а+2d)+(а+3d)+(а+5d)=51

3а+10d=51

3a=51-10d

a=(51-10d)/3

Підставимо (51-10d)/3 замість а у рівність (а+7d)-8/(а+d)=2.

((51-10d)/3 +7d-8)/( (51-10d)/3+d)=2

(51-10d)/3 +7d-8=( (51-10d)/3+d)*2

17-3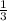 $\frac{1}{3}$ d+7d-8=(17-3 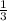$\frac{1}{3}$ d+d)*2

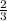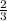9+3 $\frac{2}{3}$ d=34-4 $\frac{2}{3}$ d

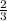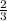3 $\frac{2}{3}$ d+4 $\frac{2}{3}$ d=34-9

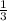8 $\frac{1}{3}$ d=25

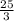
d=25/ $\frac{25}{3}$

d=3

Знайдемо а:

а=(51-10*3)/3=21/3=7

Тоді сьомий член арифметичної прогресії:

а+6d=7+6*3=25

Відповідь: 25

MOGZ ответил